Epatez
les copains avec ce tour : vous passerez pour un génie du calcul
!
Procédure
Demander
à un ami d'écrire deux nombres sur une feuille de papier.
Ces deux nombres ne devront pas être trop grands pour ne pas
avoir trop de travail.
L'idéal est de noter ces deux nombres dans les deux cases du
haut en gauche du L colorié en jaune dans la grille ci-dessous.
Il suffit de préparer à l'avance plusieurs grilles de
ce type pour répéter le tour.
 |
Prenons
par exemple les deux premiers nombres, 17 et 20.
Demander alors d'écrire en dessous, le résultat
de la somme de ces deux nombres.
Ici c'est 37.
Recommencer selon la même procédure jusqu'à
la dernière case jaune.
Chaque nombre écrit est la somme des deux nombres
précédents.
Cela rappelle la construction de la suite de Fibonacci...
Vérifier que votre ami a bien réalisé ce
qui est demandé.
Alors vous
lui demandez de faire la somme des dix nombres inscrits.
Et comme vous êtes sympathique vous lui proposez votre
calculatrice.
|
 |
Pendant ce temps,
vous inscrivez rapidement le résultat sur une feuille de papier
que vous tendez à votre ami.
Laissez le terminer
son calcul sur la calculatrice avant de regarder votre feuille.
Il est alors stupéfait devant l'exactitude du résultat
que vous avez noté bien avant lui...
Le
secret de la réussite
Le résultat
est égal à 11 fois le
septième nombre de la suite à partir
du haut.
Ce nombre est situé dans le coin gauche en bas de la grille.
La disposition en L ne fait que faciliter la lecture de ce septième
nombre.
Ci-dessus, la somme
17 + 20 + 37 + 57 + 94 + 151 + 245 + 396 + 641 + 1037 =
2695
est égale à 11 fois 245.
C'est aussi 245 x 11 = 2695
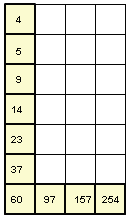
Ci-contre, la somme
4 + 5 + 9 + 14 + 23 + 37 + 60 + 97 + 157 + 254 =
660
C'est aussi 60 x 11 = 660 |
|
Il est très
facile de multiplier un nombre par 11.
On utilise la distributivité de la multiplication
par rapport à l'addition.
En effet 11 = 10 + 1.
Ainsi 245 x 11 = 245 x (10 +1) = (245 x 10) + (245 x 1)
=
2450 + 245
=
2695.
De même 60 x 11 = 600 + 60
= 660.
Pour multiplier un nombre n par 11, on
le multiplie par 10 et on ajoute ce nombre n au résultat de
la multiplication par dix.
La multiplication par 11 fait partie du calcul mental à connaître
en CM2.
Il existe dans les livres de nombreuses astuces pour obtenir le résultat.
Personnellement, j'utilise toujours la multiplication par 10 suivie
de l'addition. C'est simple et logique.
Justification
Pour
ceux que cela intéresse nous
allons démontrer pourquoi la somme est exactement égale
à 11 fois le septième nombre de la suite.
Soient m et n les deux premiers nombres proposés par votre
ami.
Le premier nombre est m ;
le deuxième nombre est n.
Alors le troisième nombre est m+n
;
le quatrième nombre est (m+n)
+ n = m + 2n ;
le cinquième nombre est (m
+ 2n) + (m+n) = 2m + 3n ;
le sixième nombre est (2m
+ 3n) + (m
+ 2n) =
3m + 5n ;
le septième nombre est (3m
+ 5n) + (2m
+ 3n)
= 5m + 8n ;
le huitième nombre est (5m
+ 8n) + (3m
+ 5n) =
8m + 13n ;
le neuvième nombre est (8m
+ 13n) + (5m
+ 8n) =
13m + 21n ;
le dixième nombre est (13m
+ 21n) + (
8m + 13n) = 21m + 34n.
Le total des dix nombres est égal à 55m
+ 88n = 11 (5m + 8n).
Le total des dix nombres est bien égal
à 11 fois le septième nombre.