Du cercle inscrit à Pythagore

2 ab = (a + b + c) d a² = b² + c² 2 ab = (a + c - b) ( b + c - a)

D.G Rogers m'a envoyé son article : from inscribed circle to Pythagorean proposition.
Avec son autorisation, je vous le propose ici.. Les animations mettent en évidence les astucieuses démonstrations géométriques.

Soit un triangle rectangle dont les côtés de l'angle droit mesurent a et b, l'hypoténuse mesure c.
Deux expressions mathématiques mettent en relation le rayon du cercle inscrit dans un triangle rectangle et la mesure des longueurs des deux côtés de l'angle droit : .

2ab = (a+b+c)d

Si l'on pose d = 2r, chacune des deux animations montre que 2ab = (a+b+c)d.



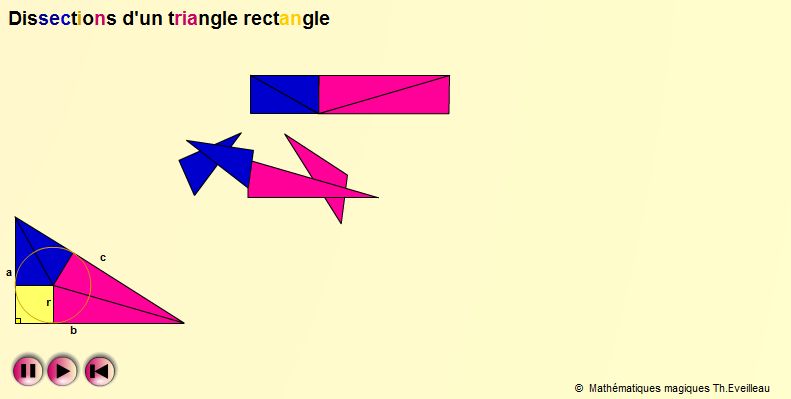
Le puzzle animé

Cette première animation démonte le triangle rectangle comme un puzzle pour obtenir la formule : 2ab = (a+b+c)d.

CLIQUER

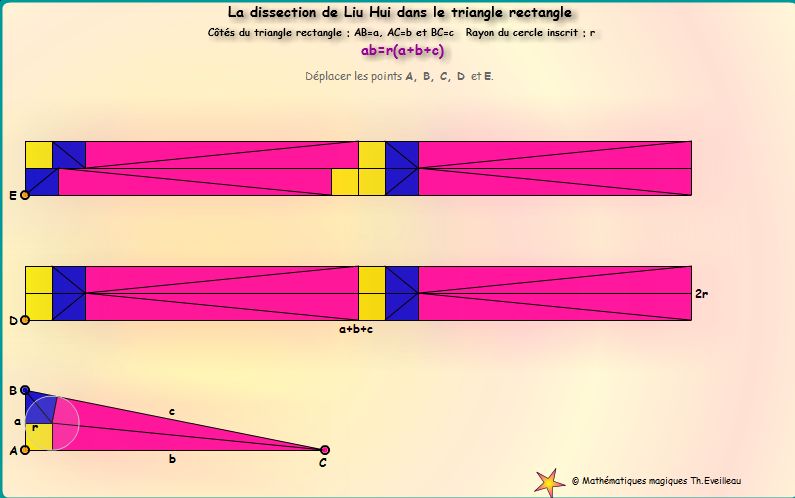
L'animation suivante permet de modifier les dimensions du triangle rectangle

Déplacer les points A, B, C, D et E avec la SOURIS ou bien au CLAVIER.

Flèches Haut et Bas pour les quatre points A, B, D et E.
Flèches Gauche et Droite pour le point C.

Les mesures des trois côtés du triangle inscrit :
AB = a ;
AC = b   et
BC = a.

Les deux grands rectangles ont pour longueur : a+b+c et pour largeur d=2r.
L'aire de deux triangles rectangles est égale à celle de chacun des grands rectangles.

Et    2ab = (a+b+c)d

Ceci est d'ailleurs un cas particulier de la formule générale :
pr=S où pest le demi-périmètre du triangle et S la surface de cce triangle.dans un triangle quelconque.

a² + b² = c²

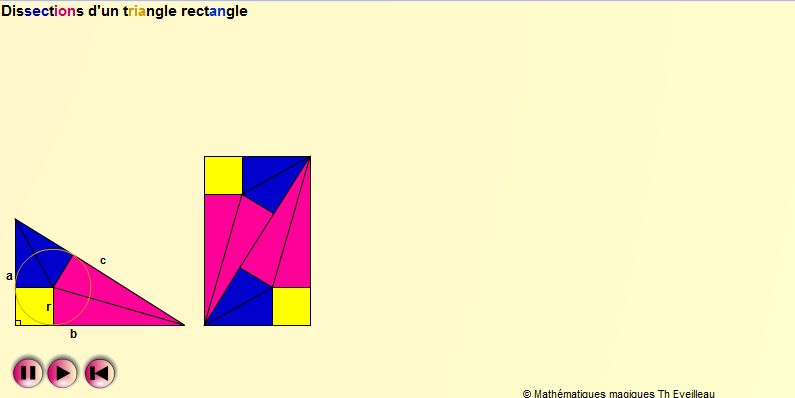
Le puzzle

Cette animation démonte le triangle rectangle comme un puzzle pour obtenir la formule : a² + b² = c².

 

CLIQUER

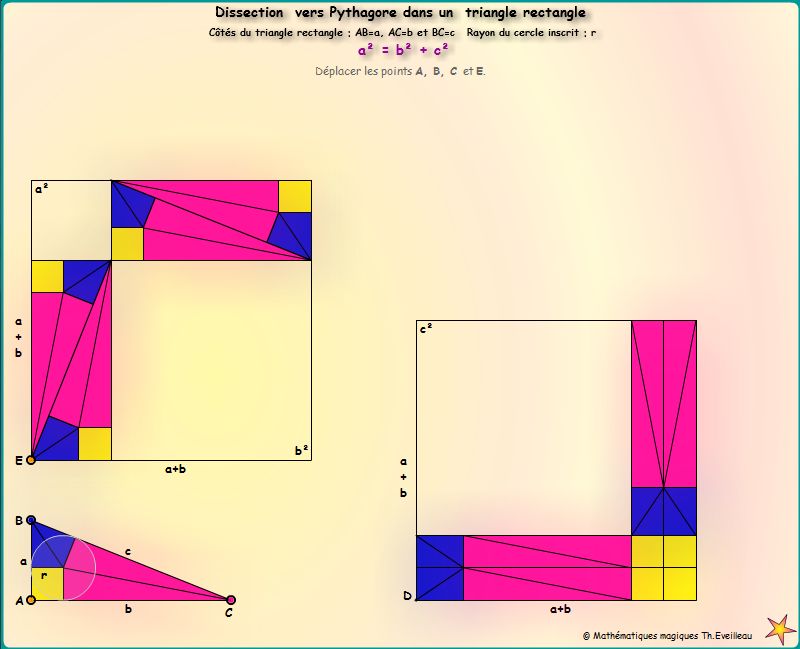
L'animation suivante permet comme de modifier les dimensions du triangle rectangle

Déplacer les points A, B, C et E avec la SOURIS ou bien au CLAVIER.

Flèches Haut et Bas pour les trois points A, B et E.
Flèches Gauche et Droite pour le point C.

 

Les carrés a², b², c² ont pour côté les trois côtés du carré.
Et nous avons bien a² + b² = c².

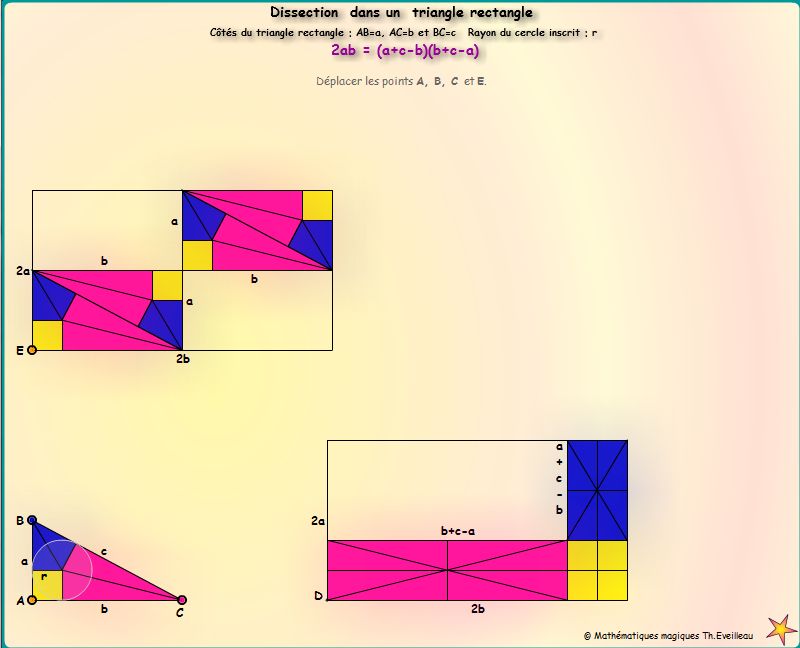
2ab = (a + c - b)(b + c - a)

Nous glissons les vingt pièces dans un rectangle de côtés 2a sur 2b.

Le puzzle montre que dans le triangle rectangle de côtés a, b et d'hypoténuse c on a :
2ab = (a + c - b)(b + c - a).

CLIQUER

L'animation suivante permet comme de modifier les dimensions du triangle rectangle

Déplacer les points A, B, C et E avec la SOURIS ou bien au CLAVIER.

Flèches Haut et Bas pour les trois points A, B et E.
Flèches Gauche et Droite pour le point C.

 

CLIQUER

Les deux rectangles montrent bien l'égalité 2ab = (a + c - b)(b + c - a).

 

---