Additionner des nombres entiers

Combien font 1 + 2 + 3 + 4 + ... + 11 ?

GAUSS (né le 30 avril 1777 à Brunswick et mort le 23 février 1855 à Göttingen)
La légende raconte qure Gauss aurait trouvé seul la méthode de sommation des entiers (1+2+…+n=n(n+1)/2).
L'origine de ce mythe est l'éloge funèbre de Wolfgang Sartorius : « Le jeune Gauss venait juste d'arriver dans cette classe quand Büttner donna en exercice la sommation d'une suite arithmétique. À peine avait-il donné l'énoncé que le jeune Gauss jeta son ardoise sur la table en disant « la voici ». Tandis que les autres élèves continuaient à compter, multiplier et ajouter, Büttner, avec une dignité affectée, allait et venait, jetant de temps en temps un regard ironique et plein de pitié vers le plus jeune de ses élèves. Le garçon restait sagement assis, son travail terminé, aussi pleinement conscient qu'il devait toujours l'être, une fois une tâche accomplie, que le problème avait été correctement résolu et qu'il ne pouvait y avoir d'autre réponse. »

Cette histoire est peut-être exagérée, cependant Carl Friedrich Gauss a fait avancer de façon considérable les mathématiques. Il est aujourd’hui considéré comme l’un des plus grands génies de l’histoire.

CLIQUER

AUTRE animation
Imaginons que l'on mette l'une à côté de l'autre des piles de 1, 2, 3, 4... 11 cubes verts.
On forme ainsi un escalier. Pour compter les cubes constituant l'escalier vert, on le complète à gauche avec un escalier symétrique marron.
Nous obtenons ainsi un rectangle de 11 sur 12 carreaux.
Le nombre de cubes verts est donc de (11 x 12) / 2.

Regardez bien la figure ci-dessous, en tirant à gauche puis à droite, le point .Pilote.
Vous verrez ainsi apparaître la somme des premiers entiers.

Déplacet le point Pilote dans l'animation.

                                                         

CLIQUER

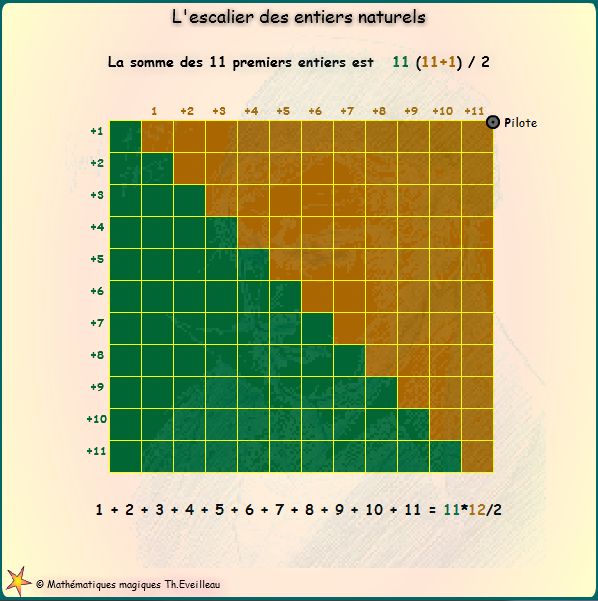
La somme des n premiers nombres entiers est n(n+1)/2.

 

Le calcul de Gauss
A l'école élémentaire, où sa mère l'envoya, le professeur de Karl Friedrich Gauss fut stupéfait par la virtuosité de ce gamin de huit ans. En effet il avait demandé à ses élèves de calculer la somme des cent premiers nombres entiers afin de souffler un peu.
Karl Friedrich Gauss écrivit alors fébrilement sur son ardoise et, quelques secondes plus tard annonçait le résultat. Il avait tout simplement écrit deux fois de suite la suite des nombres mais en ordre inverse :
1 + 2 + 3 + ... + 99 + 100
100 + 99 +... + 3 + 2 + 1
Ainsi en groupant les nombres deux par deux verticalement, il obtenait à chaque fois une somme de 101, ceci 100 fois puisqu'il y avait 100 nombres. Le double de la somme cherchée était donc de 100x101. Finalement il trouva (100 x 101) / 2 =5050.
Quelques années plus tard, K.F. Gauss était surnommé "Le prince des mathématiciens" car il multiplia les idées géniales et les découvertes dans tous les domaines des mathématiques, de la physique et de l'astronomie.

 

  Applications Poignées de mains

50 personnes se réunissent et se saluent toutes en échangeant une poignée de mains.
Combien de poignées de mains sont ainsi échangées ?
Et avec n personnes ?

Solution 

.Chacune des personnes donne 49 poignées de mains, il y a 50 personnes. Cela fait 50 fois 49 poignées de mains. Mais chaque poignée est comptée deux fois (car 2 personnes échangent la même).  Le résultat est donc (49 x 50) /2 . Dans le cas général, on trouve : (n-1)(n)/2 .Autre façon de procéder : -la première personne donne 49 poignées de mains. -la deuxième personne donne 48 poignées de mains. -la troiième personne donne 47 poignées de mains. . -la dernière donne 1 poignée de mains. On obtient ainsi : 49 + 48 + 47 + ... + 1 qui est égal comme on l'a vu à (49 x 50) / 2

 

 

Segments

16 points sont tracés sur une feuille, de façon à ce que 3 quelconques d'entre eux ne soient jamais alignés. Combien peut-on tracer de segments les joignant 2 à 2 ? Et avec n points ?

Solution 
Si l'on considère chaque point comme une personne et chaque trait comme une poignée de mains, le problème est le même que le précédent.
Pour 16 points, il y a (15 x 16)/2 segments.
Pour n points, il y a (n-1)(n)/2 segments.

 

   

Un 1 malicieux (Niveau lycée)

Le 1 malicieux prétendait qu'il égalait tout nombre entier aussi grand fût-il.
Et il le démontrait ainsi :
ci-dessus, nous avons vu que
  1 + 2 + 3 + ... + n = 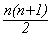      (F1)
En ajoutant les entiers jusqu'à (n-1) au lieu de n, on obtient :
1 + 2 + 3 + ... + (n-1) =         (F2)

En ajoutant 1 dans chaque membre de (F2), on obtient :
1 + 2 + 3 + ... + (n - 1) + 1 = + 1
1 + 2 + 3 + ... + (n - 1 + 1) = + 1
1 + 2 + 3 + ... + n = + 1
En utilisant le résultat de (F1), on obtient :
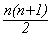= + 1
Soit
n(n+1) = (n-1)n + 2
n² + n = n² - n + 2
n + n = 2
2 n = 2
n = 1

Et 1 égale tous les entiers !

Explication 
Pas de panique ! Il y a effectivement escroquerie : Il faut se méfier des points de suspension. Ici, ils signifient que l'on écrit tous les entiers compris entre...

Ainsi nous n'avons pas d'égalité entre
1 + 2 + 3 + ... + (n - 1) + 1
              ET
1 + 2 + 3 + ... + n

Oui bien sûr, l'addition est associative, mais écrivons les derniers termes avec l'interprétation faite ci-dessus des points de suspension :

1 + 2 + 3 + ... + (n - 1) + 1 = 1 + 2 + 3 + ... + (n - 2) +(n - 1) + 1
             ET
1 + 2 + 3 + ... + (n - 1 + 1) = 1 + 2 + 3 + ... + n
                                            = 1 + 2 + 3 + ... + (n - 2) +(n - 1) + n

Les derniers termes des expressions ci-dessus ne sont pas identiques et l'on voit comment 1 devient n. L'erreur est dévoilée.