Thalès (-648,-637) fut sans doute l'un des fondateurs des mathématiques grecques, un savant universel, curieux de tout, cherchant à découvrir et expliquer le monde. Il était très proche des conceptions modernes de la science :
Pourquoi en est-il ainsi ? Pourquoi cela fonctionne-t-il ?
Invité par le roi Amasis, averti de ses grandes connaissances il se montra à la hauteur de sa réputation : le roi déclarait ne pas connaître la hauteur des fantastiques pyramides déjà presque bimillénaires. Thalès eut de la chance : il planta sa canne dans le sable verticalement et dit au roi : "l'ombre de ma canne est exactement égale à sa hauteur; il doit en être de même pour votre pyramide : faites mesurer son ombre vous aurez sa hauteur !"
Bien plus tard, à la fin du XIXe siècle, on appellera en France, "de Thalès" le théorème qui porte aujoud'hui ce nom.
Si deux triangles ABC et A'B'C' ont leurs côtés parallèles, alors on a:
AB/A'B'=AC/A'C'=BC/B'C'
En Allemagne, le théorème dit de Thalès en est un autre:
Un triangle inscrit, dans un cercle et ayant pour côté un diamètre du cercle est rectangle. Et réciproquement un triangle rectangle est inscrit, dans un demi-cercle.
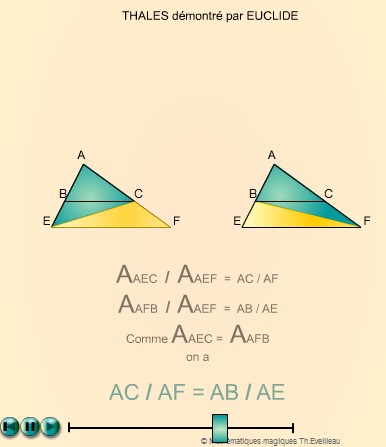
Pourtant c'est Euclide (école d'Alexandrie -350) qui démontra ce théorème dans Les Eléments, livre VI. Dans ce livre il applique la théorie des proportions d'Eudoxe qu'il applique à la proportionnalité sur des longueurs ou des angles et aux triangles semblables.
Voici la démonstration du théorème dit de Thalès par Euclide, revue et animée selon l'an 2003.
(1)
Histoire de la Science de Pierre Rousseau ed Fayard, 1945
Histoire des Mathématiques par J.-F. Montucla, An VII-rééd. Blanchard