Le gnomon  

"A thing enabling something to be known, observed or verified"                                                                                   Thomas L. Heath

Additionner des impairs Extraire une racine carrée Gnomon ?

 

 

Additionner des nombres entiers impairs

Combien font 1 + 3 + 5 + 7 + ... ?
Regardez bien la figure ci-dessous, en tirant à gauche puis à droite, le point .Pilote.
On ajoute les disques par groupe de couleur :
              1 marron,
              3 verts,
              5 marrons,
              7 verts.
On trouve que la somme des 4 premiers nombres impairs est le carré de 4, soit 16 :
              1 + 3 + 5 + 7 = 4²

Déplacet le point Pilote dans l'animation.

                                                                                                    

CLIQUER

 

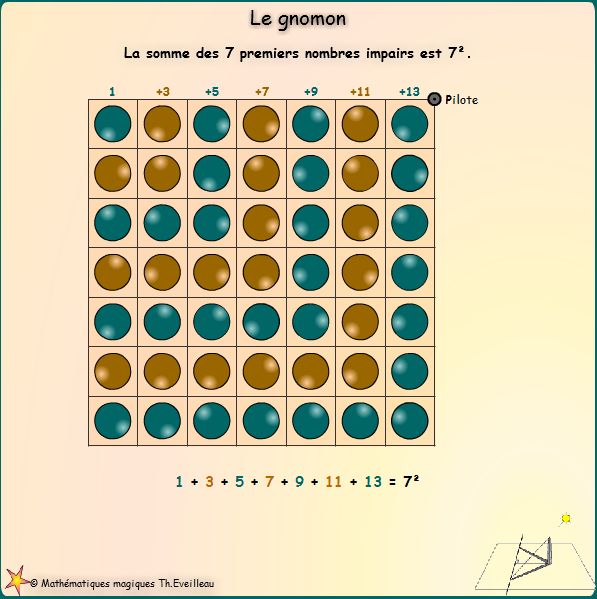
De façon générale la somme des n premiers nombres impairs est n2.

On obtient l'expresson générale : 1 + 3 + 5 + 7 + 9 + 11 + ... + (2n + 1) = ( n + 1) 2

 

Extraire la racine carrée d'un carré parfait
ou donner une valeur approchée pour un entier quelconque.
Pour avoir la racine carrée d'un nombre qui est un carré parfait, il suffit de procéder à l'envers :
On soustrait la suite des nombres impairs à partir de 1, jusqu'à l'obtention d'un résultat nul.
On compte alors le nombre d'entiers enlevés.
Le résultat donne la racine carrée.

             

16 - 1 = 15 15 - 3 = 12 12 - 5 = 7 7 - 7 = 0 Il y a 4 soustractions Donc la racine carrée de 16 est 4.

 Pour avoir la racine carrée d'un nombre quelconque, on procède de même jusqu'à ce qu'on ne puisse plus obtenir un nombre positif. On compte le nombre d'entiers enlevés et l'on a une valeur approchée à une unité près par défaut, du résultat.

              

106 - 1 = 105 105 - 3 = 102 102 - 5 = 97 97 - 7 = 90 90 - 9 = 81 81 - 11 = 70 70 - 13 = 57 57 - 15 = 42 42 - 17 = 25 25 - 19 = 6 Il y a 10 soustractions Donc la racine carrée de 106 est 10 à 1 près par défaut.

Evidemment nos calculettes sont plus rapides et efficaces, mais ce procédé très ancien reste très simple.

Gnomon : les débuts de la géométrie en Grèce

Texte de Michel Serres
"Nous avons du mal à traduire le mot gnomon parce qu'il vibre d'harmoniques autour de la chose qu'il désigne et que la connaissance scintille à la pointe de son axe...
Littéralement, il signifie, sous une forme apparemment active : qui discerne, qui règle, mais désigne toujours un objet. Dans son commentaire à la deuxième définition du second livre d'Euclide, Thomas L. Heath le décrit comme "a thing enabling something to be known, observed or verified", une chose permettant à quelque chose d'être connu, observé ou vérifié. Le voisinage de ces deux choses ou leur répétition a du sens : elles ont rapport entre elles, toutes seules. En cette chose ou par elle, au lieu qu'elle occupe, le monde montre la connaissance...
Comme l'axe du cadran se dressait perpendiculaire à son plan, l'expression "à la manière du gnomon" exprimait chez les Grecs, à une période archaïque, l'angle droit ou le fil à plomb. Du coup, nous pourrions presque le traduire par règle ou équerre, d'autant qu'Euclide, au lieu indiqué, appelle gnomon les aires des parallélogrammes complémentaires d'un parallélogramme donné, de sorte que leur addition ou soustraction les laissent ensemble semblables entre eux. Ainsi, une équerre montre deux rectangles ou deux carrés complémentaires d'un carré ou rectangle donné: le mot français lui-même semble signifier l'extraction du carré ou cadran."