Les ensembles de Julia et de Mandelbrot

---

.Un peu d'histoire et de mathématiques Les ANIMATIONS .Ensembles de Mandelbrot .Ensembles de Julia

---

La nature est-elle fractale ? "La géométrie fractale changera profondément votre vision des choses. Il est dangereux de continuer cette lecture. Vous risquez de perdre définitivement l'image inoffensive que vous avez des nuages, des forêts, des galaxies, des feuilles, des plumes, des fleurs, des roches, des montagnes, des tapis et bien d'autres choses encore..." Michael Barnsley, professeur de l'université nationale d'Australie dans Fractals Everywhere

*****

Les concepts mathématiques présentent une réalité bien plus profonde que l'apparence matérielle.

Depuis toujours les hommes montrent de la curiosité à comprendre les lois de l'univers.
La nature construit des structures en appliquant un principe d'économie. Elle crée un modèle architectural et le répète à différentes échelles à l'intérieur et en dehors de l'objet. Par exemple le système de ramification des plantes.

On pense même que dans un état de bonne santé, le corps est en situation chaotique et que dans la maladie le corps adopte un état de réponses répétitives. La maladie fait que le corps perd de sa complexité et donc perd son comportement fractal.

Les fractales mathématiques possèdent la propriété d'autosimilarité, elles sont donc infiniment complexes quelle que soit l'échelle d'observation.

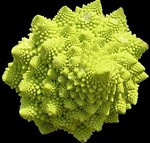
Toutefois dans la nature, tout n'est pas aussi parfait. On ne peut comparer un objet à une fractale idéale mathématique que pour quelques niveaux de zoom. Le chou romanesco en est un exemple étonnant.
Le chou entier (niveau 1) est formé de copies alignées en spirale (niveau 2).
Chacune est composée de d'autres copies aussi disposées en spirale (niveau 3).
Le phénomène se reproduit de nouveau une dernière fois (niveau 4) .

Les fractales commencent à peine à être explorées et constituent une manière assez nouvelle de voir le monde.

Un peu d'histoire et de mathématiques

Gaston Julia (1893-1978) fut un précurseur de l'étude des fractales.
Spécialiste des fonctions d'une variable complexe. Ses résultats de 1917-1918 sur l'itération des fractions rationnelles ont été utilisés, dans les années 1970, par Benoît Mandelbrot.

Mandelbrot est né en Pologne en 1924 (mort à Cambridge le 14 octobre 2010) et émigra en France en 1936 chez son oncle Szolem membre fondateur du groupe Bourbaki.
En 1945 il lut sans trop d'intérêt un ouvrage de Julia intitulé "Mémoire sur l'itération des fonctions rationnelles". Cependant en 1970, au moyen d'ordinateurs d'IBM aux Etats-Unis, il réalisa des illustrations d'un essai qui surprit la communauté scientifique par les détails d'un graphique qui sera baptisé "l'ensemble de Mandelbrot".
Mandelbrot mit ainsi en avant la géométrie fractale, une nouvelle forme de pensée dans les domaines des mathématiques et des sciences naturelles. Il a conçu des méthodes d'observation basées sur l'autosimilarité.
Mandelbrot montra que de nombreuses structures naturelles apparemment très complexes présentent en réalité une régularité géométrique invariante à différentes échelles. Il publia "The Fractal geometry of Nature" en 1982.

Une fractale est le produit final obtenu par la répétition infinie d'un processus géométrique bien défini.
Quel que soit le niveau d'observation, on constate qu'il existe un modèle qui se répète sans que l'échelle d'observation ait une quelconque importance.
Le procédé est généralement très simple. En raison de l'itération infinie, on obtient des structures d'une complexité extraordinaire.

Les fonctions utilisées par Julia puis par Mandelbrot
Les ensembles de Julia et de Mandelbrot sont étroitement associés.
Ils sont surprenants par leur complexité et leur beauté.

Z étant une variable complexe, on construit la suite récurrente définie par
Zn+1 = Zn² + C.

Cette expression est très intéressante lorsque Z représente un nombre complexe : Z = a + ib.
Ce nombre complexe Z est représenté dans le plan par un point d'abscisse a et d'ordonnée b.

Si Z = a + ib et Z' = a' + i b'
Rappelons que l'addition est définie par
Z + Z' = (a + a' ) + i (b + b')

et la multiplication par
Z Z' = (aa' - bb') + i (ba' + ab')
car i² = -1.

Cette suite a d'abord été étudiée par Gaston Julia.
Peu chanceux, Julia se cachait le visage en partie, car il fut blessé à la tête pendant la première Guerre mondiale.
Il mourut sans connaître la notoriété en 1978 malgré ses importantes découvertes car les ordinateurs de son époque n'étaient pas graphiquement assez puissants.

Des années plus tard, Mandelbrot étudia l'expression Zn+1 = Zn² + C, avec un ordinateur et ainsi continua le travail entamé par Gaston Julia.
Il explora l'utilité des fractales dans différents domaines notamment en physique et en économie.
Le terme de fractale fut inventé en 1975.
En étudiant les ensembles de Julia, il découvrit ceux qui portent son nom : les ensembles de Mandelbrot.

 Ensemble de Mandelbrot

Ce que l'on appelle "ensemble de Mandelbrot" est un ensemble obtenu par une simple relation de récurrence avec une élévation d'un nombre complexe au carré.

On analyse la suite
Zn+1 = Zn² + C.
Dans l'ensemble de Mandelbrot, on analyse ce que l'on appelle l'orbite 0.
C'est-à-dire qu'on étudie l'itération répétitive de l'expression Zn+1 = Zn² + C dans le cas particulier où Z0 = 0.

Dans l'animation suivante,
l'ensemble des images dans le plan, des valeurs de C où l'orbite résultante ne va pas jusqu'à l'infini, est colorié d'une certaine façon selon le temps d'échappement. Cet ensemble de valeurs de C reçoit précisément le nom d'ensemble de Mandelbrot.
Les autres valeurs de C donneront des points coloriés en noir.

Dans l'animation ci-dessous,
     ..On peut faire varier le paramètre de couleur de 0 à 255, pour obtenir une couleur différente : plus ou moins de vert.
        Penser à frapper la touche ENTREE si le nombre est entré au clavier.
     .On peut zoomer de nombreuses fois une zone choisie que l'on délimite avec la souris.
     .Cliquer le bouton RéInitialiser lorsque les contours sont très lissés :
       alors le zoom atteint quelques milliards... et on atteint les limites du calcul sur l'ordinateur.

Si nous approchons d'une zone quelconque de l'ensemble, et si nous zoomons, nous voyons que les mêmes figures sont reproduites à plusieurs reprises. Chaque agrandissement d'une partie est semblable à l'ensemble total : c'est le caractère fractal.

 

 

Ensembles de Julia

Dans les ensembles de Julia, on analyse la suite de nombres complexes,
Zn+1 = Zn² + C dans le cas où C est une constante..

L'ensemble des valeurs de Z où l'orbite (i.e la suite des valeurs obtenues) ne tend pas vers l'infini est colorié d'une certaine façon selon le temps d'échappement vers l'infini, les autres en noir.

Dans l'animation suivante,
    .On peut faire varier le paramètre de couleur de 0 à 255, pour obtenir une couleur différente : plus ou moins de vert.
             Penser à frapper la touche ENTREE si le nombre est entré au clavier.
    .On peut faire varier la valeur de la constante complexe C. Pour cela on entre deux valeurs : partie réelle et partie imaginaire.
            Voici quelques valeurs intéressantes :
            0.285 et 0.01 ; 0.13 et 0.745 ; 0.4 et 0.2 ;  -1 et 0 ;
            0.5 et 0.5 ; 0.3 et 0.5 (lapin de Julia) ; -0.72 et 0.11 ; 0.185 et 0.013
            Ne pas hésiter à essayer de nombreuses valeurs.
     .On peut zoomer de nombreuses fois une zone choisie que l'on délimite avec la souris.
     .Cliquer le bouton RéInitialiser lorsque les contours sont très lissés :
             alors le zoom atteint quelques milliards... et on atteint les limites du calcul de mon programme.

Observer le jeu des couleurs et l'autosimilarité des formes.