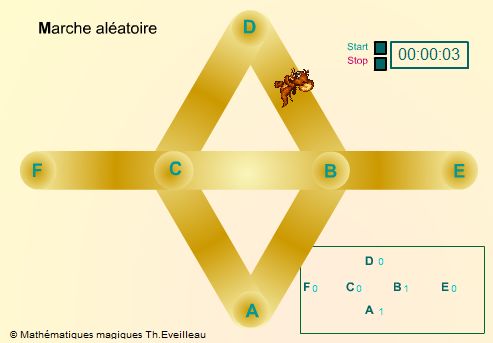
Une souris se déplace sur un circuit. Pour aller d'une lettre à l'autre elle met deux secondes. A chaque carrefour elle peut repartir indifféremment dans une direction ou l'autre. Ainsi quelle que soit la façon dont elle est arrivée en B elle aura une chance sur quatre de continuer vers C, A, E ou D.
Dans l'animation suivante, il suffit de cliquer sur start, pour voir s'afficher selon le temps écoulé les nombres de passages sur les différentres lettres.
CLIQUER
Exemples
Probabilité en partant de D d'arriver en A en 4 secondes donc en 2 fois.
Les chemins possibles sont ceux de longueur 2 donc :
DBA, DCA.
Pour le trajet DBA la probabilité est 1/2x1/4.
La probabilté P en partant de D pour arriver en A en 2 fois est :
P = 2(1/2x1/4)
P = 1/4
Les chemins possibles sont ceux de longueur 3 donc :
DCBA, DBCA.
Pour le trajet DCBA la probabilité est 1/2x1/4x1/4.
La probabilté P en partant de D pour arriver en A en 3 fois est :
P = 2(1/2x1/4x1/4)
P = 1/16
Les chemins possibles sont ceux de longueur égale ou plus petite que 4 donc :
DBA, DCA, DCBA, DBCA, DBEBA, DCFCA, DBDBA, DCDCA.
Pour le trajet DBA ou bien DCA la probabilité est 1/2x1/4.
Pour le trajet DCBA ou bien DBCA la probabilité est 1/2x1/4x1/4.
Pour le trajet DBEBA ou bien DCFCA la probabilité est 1/2x1/4x1x1/4.
Pour le trajet DBDBA ou bien DCDCA la probabilité est 1/2x1/4x1/2x1/4.
Et les chemins avec aller retour :
DBCBA ou bien DCBCA avec la probabilité 1/2x1/4x1/4x1/4
DBDCA ou bien DCDBA.avec la probabilité 1/2x1/4x1/2x1/4
Finalement la probabilté P en partant de D pour arriver en A en moins de 4 secondes est :
P = 2(1/2x1/4) + 2(1/2x1/4x1/4) + 2(1/2x1/4x1x1/4) + 2(1/2x1/4x1/2x1/4) + 2(1/2x1/4x1/4x1/4) + 2(1/2x1/4x1/2x1/4)
P = 1/4 + 1/16 + 1/16 + 1/32 + 1/64 + 1/32
P = 29/64
Par des procédés utilisant des théories plus compliquées le mathématicien Markov montre par exemple que la probabilité de ne jamais arriver sur une case est nulle.
