La montgolfière est construite avec des octogones réguliers inscriptibles dans des cercles supportés par une sphère.
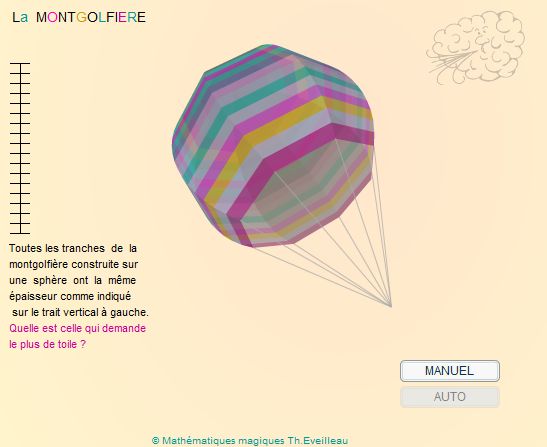
Toutes les tranches de couleur ont la même épaisseur comme indiqué sur le segment vertical.

Quelle est la bande qui nécessite le plus de toile ?
L'animation peut être lancée de façon AUTOmatique ou MANUELlement en suivant les indications proposées.

CLIQUER

SOLUTION


Aussi surprenant que cela puisse paraître les tranches ont toutes la même aire et
la quantité de toile est la même pour chaque bande de couleur.

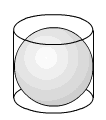En effet l'aire de la surface de chaque tranche sphérique est la même que celle de la tranche correspondante d'un cylindre dont la base est un disque de même diamètre que la sphère. Il est évident que dans un cylindre les tranches ont toutes la même surface latérale. Pour la montgolfière construite avec des cotogones, l'aire de chaque bande sera la même que celle d'une bande de même épaisseur d'un prisme à base octogonale.

Archimède avait déjà trouvé ce résultat.
L'inclinaison compense exactement la largeur des tranches.

Nous allons le démontrer pour une sphère de rayon R avec une petite intégrale de niveau fin de lycée.
La démonstration fonctionne également pour les octogones.
Il suffit de remplacer le périmètre d'un cercle : 2 R , par celui d'un octogone régulier : .

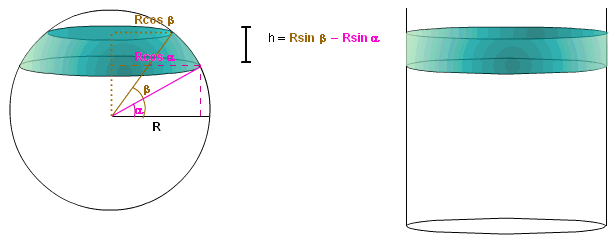
L'aire de la partie verte du cylindre est égale à 2 R h

Calculons l'aire de la partie verte de la sphère
On intègre le périmètre du cercle (soit 2 R cos ) sur la hauteur considérée comme très petite.

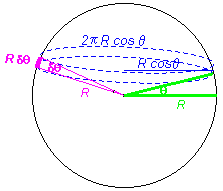
L'aire de la partie verte de la sphère est égale à 2 R h

Comme toutes les bandes de couleur ont la même épaisseur h, on en déduit que toutes ont la même aire.
C'est la même démonstration pour la montgolfière : toutes les bandes de couleur ont la même aire.

Pour la montgolfière nous obtenons

L'aire de la partie verte de chaque tranche d'épaisseur h est égale à h