Mirifiques
paraboles
 Le
poids économique du paraboloïde
Boules,
balles et ballons font de la sphère une forme géométrique
très commune sur notre bonne vieille terre ronde.
Pourtant une autre forme vient sérieusement concurrencer
économiquement la sphère. Il s'agit du paraboloïde
de révolution !
C'est tout simplement la forme de la cavité des phares quels
qu'ils soient, des voitures, des camions...
C'est aussi la forme des antennes dites 'paraboliques', des grands
détecteurs d'ondes pointés sur les profondeurs du
cosmos...
Pourquoi
donc privilégier cette forme ?
Observons d'abord sur les phares et les antennes les remarquables
propriétés de cette forme.
Ensuite nous verrons mathématiquement ce qui justifie ces
résultats étonnants.
Les
phares de nos voitures et nos antennes paraboliques
Les
phares de nos voitures
Prenons
une lampe que l'on place à l'intérieur d'une cavité
paraboloïque. Pour mieux comprendre, nous allons couper le
phare et obtenir une section en forme de parabole.
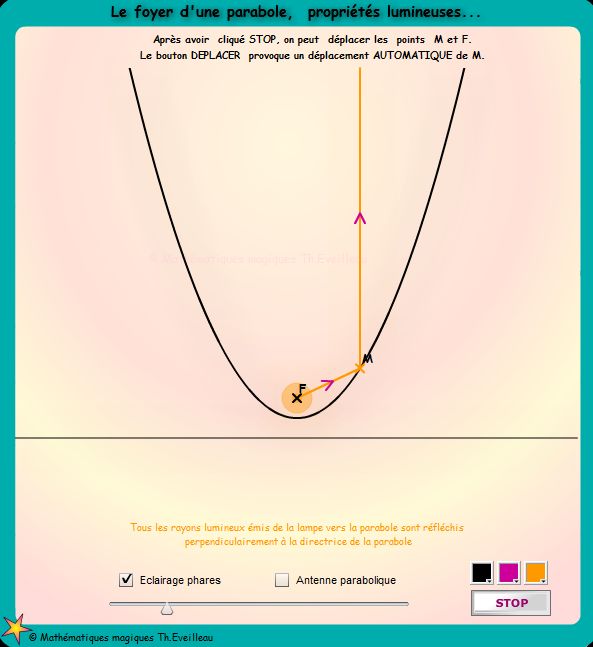
Tous les rayons lumineux émis de la lampe vers la parabole
sont réfléchis parallèlement les uns aux autres
(perpendiculairement à la droite appelée directrice
de la parabole.
C'est la meilleure situation
pour avoir un éclairage optimal.
Si les rayons partaient dans toutes les directions l'éclairage
serait inefficace.
Avec une autre forme nous ne pourrions pas obtenir le parallélisme
des rayons réfléchis.
Nos
antennes paraboliques
Dans l'animation qui suit, cocher
le bouton Antenne parabolique
Cette fois,
tous les rayons (ou les ondes ) venant d'une source éloignée
arrivent sur l'intérieur de "l'antenne parabolique".
La source est si éloignée qu'ils sont considérés
comme parallèles.
Il suffit de placer l'antenne de façon à ce que la
droite (D) (la directrice) soit perpendiculaire à ces rayons.
Après
réflexion sur l'antenne ceux-ci convergent tous vers le foyer.
Alors on peut les détecter, bien mieux qu'avec une toute
autre méthode !
Selon le choix déterminé,
- les rayons lumineux partent de la lampe (foyer) ou bien
- les ondes se concentrent vers le foyer F de la parabole.
Après réflexion sur la parabole les rayons sont toujours
perpendiculaires à la directrice de la parabole (droite
horizontale içi).
L 'animation
est automatique lorsqu'on clique le bouton DEPLACER
CLIQUER
Déréglez,
réglez l'antenne...
Ci-dessous,
l'antenne est déréglée. et
vous allez devoir l'orienter correctement pour détecter au
mieux les ondes qui arrivent.
Le meilleur moyen est de les concentrer toutes en
un seul point.
C'est possible avec le foyer de l'antenne parabolique.
La direction de ces ondes est fixe : parallèle
à l'onde verte déjà dessinée.
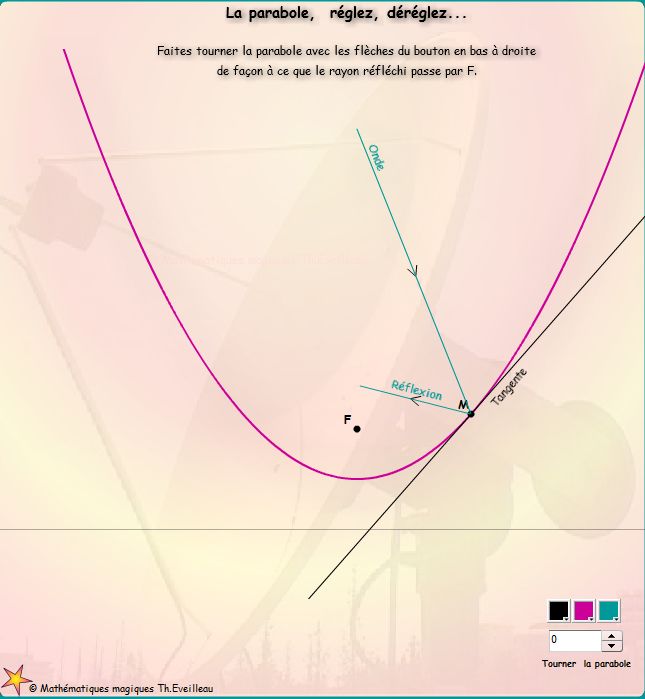
Dans l'animation suivante
On peut changer la position de l'antenne en utilisant le
bouton de rotation de l'antenne parabolique.
Elle tourne autour de son sommet.
Essayez de trouver la bonne position pour faire converger le rayon
onde et
donc ensuite tous les rayons parallèles à ce dernier,
vers le foyer F de
la parabole.
Observez alors la direction de l'onde.
ATTENTION
si vous modifiez l'angle du bouton avec le clavier, penser à
VALIDER avec la touche ENTREE
pour prendre en compte la modification.
CLIQUER
Pour concentrer tous
les rayons vers le foyer, et donc pouvoir les détecter,
il faut que les ondes arrivent
perpendiculairement à la droite directrice de la parabole.
THEOREME
.En chaque point d'une parabole il y a une tangente qui est la bissectrice
intérieure de l'angle des demi-droites joignant le point
au foyer et projetant ce point sur la directrice.
OU
Le symétrique du foyer F par rapport à une tangente
est sur la directrice.
Comprendre
Une
parabole est bien sûr définie avec l'équation
: y = ax2
+ bx
+ c
Mais
cette formule est bien abstraite et l'approche géométrique
est beaucoup plus riche.
En se donnant un point F (le foyer) et une droite fixe
(D), la directrice,
la parabole est l'ensemble des
points qui sont à égale distance de F et de la droite
(D).
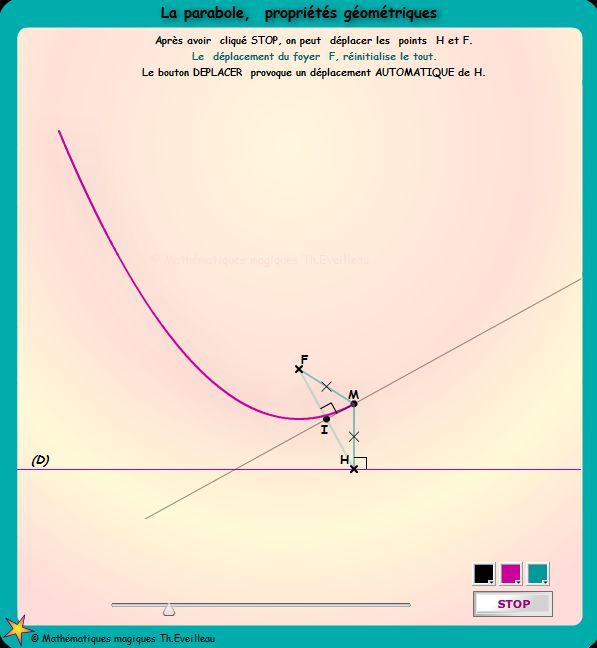
Construction :
Soit
un point F et une droite (D).
Prenons H sur la droite (D).
Traçons le segment [HF].
Traçons alors la médiatrice (IM) de [HF]
(droite perpendiculaire en son milieu ou ensemble des points équidistants
de H et de F).
Traçons la perpendiculaire à (D) en H.
Elle coupe la médiatrice en M,
qui est un point de la parabole car il est, à égale
distance de la droite (D) et de F.
La droite (IM) est tangente à la parabole. Et tout
rayon MF est réfléchi en le rayon MH.
Sur l'animation ci-dessous, après
avoir cliqué STOP, déplacer le point
H
de la droite.
Il détermine le point M équidistant
de la droite et du point F.
M décrit la parabole
-dont la directrice est la droite (D) et
-dont le foyer est le point F.
CLIQUER
|