|
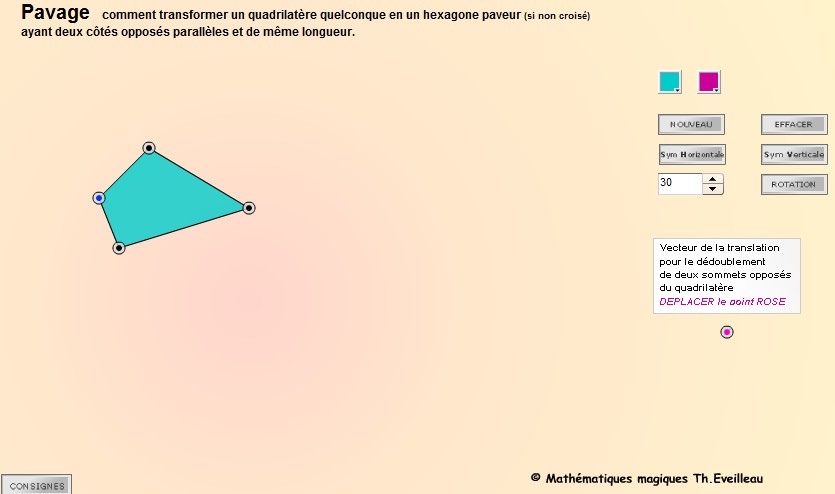
Pavage
avec des hexagones particuliers Problème
proposé avec Pierre Jullien et Diophante.fr Cette
condition SUFFISANTE est-elle NECESSAIRE ? CLIQUER
La
seule condition "avoir deux côtés opposés
parallèles et de même longueur" n'est pas suffisante. Si nous avons l'hexagone ABCDEF, tel que le côté AB soit parallèle et de même longueur que le côté ED, il faut de plus que le vecteur AB soit égal au vecteur ED. Par ailleurs le polygone ne doit pas être croisé. Cas
particulier : si l'hexagone non croisé a deux couples de côtés
opposés parallèles et de même longueur
Le troisième exemple (Hexagone P3) de l'animation fournit le cas d'un hexagone ayant trois angles de 120° et les côtés de ces angles de même mesure de longueur (deux à deux). Ce cas donne un pavage de type P3, avec une légère impression de relief. Ce pavage est réalisable parce que la somme des angles d'un hexagone est de 4x180° soit 720°. Il suffit de juxtaposer les angles analogues de 120° des différents hexagones. Ensuite, juxtaposer les trois autres angles de somme 120° correctement. Nous utilisons donc des rotations d'un tiers de tour et obtenons un pavage de type P3. Voici un exemple de ce pavage obtenu avec le troisième exemple (Hexagone P3) de l'animation précédente : 
Sur
une
proposition de Pierre, nous allons construire un hexagone paveur
en partant d'un quadrilatère quelconque. On
peut expérimenter avec l'animation suivante. CLIQUER
|


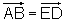 dans un hexagone non croisé ABCDEF,
dans un hexagone non croisé ABCDEF,