Les angles en radians
Prenons la droite numérique
graduée sur laquelle nous reportons les valeurs π,
π/2,
3π/2
et enfin 2π.
Traçons un cercle de rayon 1 tangent à la droite numérique
au point origine O. Nous allons enrouler la droite numérique
autour du cercle.
Sur l'animation ci-dessous, choisir les angles positifs puis les négatifs.
Pour une raison pratique d'affichage à l'écran, il n'est
pas possible d'avoir simultanément la droite numérique
positive et la droite numérique négative.
CLIQUER
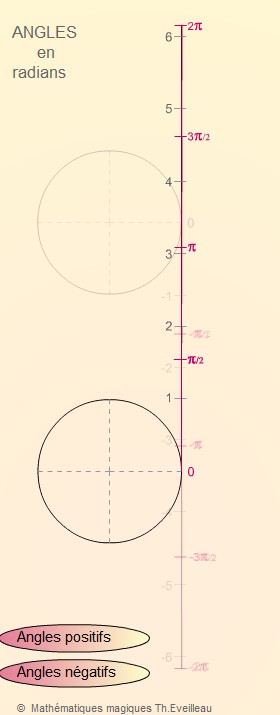
Lorsqu'on enroule
la droite numérique sur le cercle nous retrouvons les correspondances
suivantes :
- un quart de tour ou 90° correspond à un angle de π/2
radians ;
- un demi de tour ou 180° correspond à un angle de
π/2
radians ;
- trois quarts de tour ou 270° correspondent à un angle
de 3π/2
radians ;
- un tour complet ou 360° correspond à un angle de 2π
radians.
Le choix des
mesures d'angles en radians est particulièrement judicieux.
En effet, lorsqu'on choisit le rayon du cercle pour unité de
longueur, la longueur d'un arc de cercle est égale à
la mesure en radians de l'angle intercepté.
Ainsi le périmètre du cercle est 2π.
La longueur d'un quart de tour est π/2.
Celle d'un demi tour est π.
Le périmètre
du cercle
Lorsque la roue fait un tour
complet sans glisser, le contact au sol décrit une longueur
égale au diamètre multiplié par π.
Cette distance correspond au périmètre de la roue.
Dans cette figure, le rayon du cercle est choisi comme unité
1.
On peut ANIMER ou STOPPER l'animation.
Le curseur VITESSE permet d'accélérer ou de ralentir
la rotation de la roue.
Quand la roue
est arrêtée, on peut la faire rouler avec le point Contact
avec la SOURIS ou bien le CLAVIER (flèches gauche et droite).
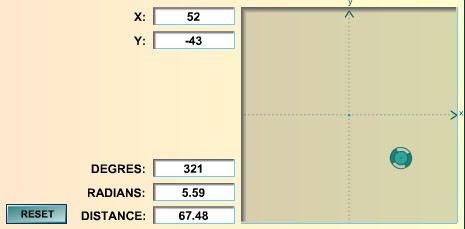
Conversions degrés,
radians
Déplacer la mire avec
la souris et observer
- ses coordonnées cartésiennes
(en x et y) ;
- ses coordonnées polaires : angle en degrés ou radians
mesurés à partir de l'axe des abscisses
dans le sens inverse des aiguilles d'une montre puis distance.
Les mesures sont arrondies au centième près.
CLIQUER
A propos
de π
:
autres jolies formules, avec des
images d'Antonio de Garcia de Pablo