Douze pièces
et une balance à fléau
ou une balance de Roberval

EXPÉRIMENTONS

Voici 12 pièces toutes identiques sauf une fausse dont on ne sait si elle plus lourde ou plus légère. En 3 pesées seulement déterminer la fausse et trouver si elle est plus lourde ou plus légère.
La balance est bloquée à chaque pesée. On place les pièces avec la souris. On pèse en cliquant sur le bouton fléché. A chaque pesée, on remet à zéro en cliquant sur le bouton RAZ. Au bout de 3 pesées, la solution est proposée si on la désire... Lorsqu'on recommence, les pièces ont de nouvelles masses.

CLIQUER

SOLUTION


On répartit les pièces en 3 paquets de 4 pièces, par exemple :
paquet A : a1, a2, a3, a4
paquet B : b1, b2, b3, b4
paquet C : c1, c2, c3, c4

CAS 1
A = B alors la fausse est dans C,
pesons (2ème pesée) d'un côté c1 et c3 avec de l'autre côté c2 et b3
si équilibre alors la mauvaise pièce est c4.
si pas d'équilibre, alors
           .si c1 et c3 plus légères que c2 et b3,
           on a deux possibilités : ou c2 plus lourde ou l'une de c1 et c3 plus légère.
           comparer (3ème pesée) c1 et c3, si elles sont égales c'est c2 qui est la plus lourde
                                              sinon la fausse est la plus légère de c1 et c3.
           .si c1 et c3 plus lourdes que c2 et b3,
           on a deux possibilités : ou c2 plus légère ou l'une de c1 et c3 plus lourde.
           comparer (3ème pesée) c1 et c3, si elles sont égales c'est c2 qui est la plus légère
                                              sinon la fausse est la plus lourde de c1 et c3.

CAS 2
A > B alors la fausse est dans A ou B,
pesons le paquet D : a1 et b1 et b2 avec le paquet E : a2 et b3 et c1.

si D < E alors la fausse est soit b1 ou b2 ou a2.
Pesons b1 avec b2, si équilibre la fausse est a2 (plus lourde) sinon c'est la plus légère de b1 et b2 car A > B.
si D = E alors la fausse est dans les pièces enlevées : soit a3 et a4 et b4.
Pesons a3 avec a4, si équilibre la fausse est b4 (plus légère) sinon c'est la plus lourde de a3 et a4 car A > B.
si D > E alors la fausse est soit a1 ou b3. On pèse a1 avec c1 (qui est bonne). Si équilibre c'est b3 (plus légère)
sinon c'est a1 (plus lourde).

CAS 3
A < B alors inverser le rôle de A et B dans le cas 2 ci-dessus.

 

SOLUTION schématisée et colorée avec Pierre Jullien

La situation est représentée par un coffret dans lequel on range les pièces selon trois lignes de quatre pièces. Nous convenons de laisser en blanc les pièces dont on ignore la nature. Lorsqu'une pièce a pu potentiellement faire pencher la balance on la colore provisoirement en bleu foncé si on la suppose plus lourde et en bleu clair si on la suppose plus légère.

Lorsqu'on est sûr qu'une pièce n'est pas fausse on la colore définitivement en jaune.

PESEE 1
On compare les trois pièces de la première ligne avec celles de la deuxième ligne.
Nous obtenons trois cas.

PESÉE 3

Pour terminer deux cas se présentent :
- deux pièces au moins sont de même couleur alors on les compare et on conclut :
  .si elles sont égales alors c'est la troisième qui est fausse :
      si cette 3ème est bleu foncé alors elle est plus lourde,
      si cette 3ème est bleu clair alors elle est alors plus légère ;
  .si elles sont de masses différentes et
      si elles sont bleu foncé, la fausse est la plus lourde,
      si elles sont bleu clair, la fausse est la plus légère.
- sinon on compare une pièce douteuse avec une jaune et on conclut :
  .si on choisit une pièce douteuse bleu foncé :
      si de même masse que la jaune, alors la bleu clair est fausse et plus légère ;
      si plus lourde que la jaune, alors elle est fausse et plus lourde.
  .si on choisit une pièce douteuse bleu clair on fait l'analyse opposée qui donnera la même conclusion.  

 

 

CAS GÉNÉRAL


PROBLEME
Nous disposons de 4x3ⁿ pièces, en apparence identiques. L'une d'entre elles est fausse : elle est plus lourde ou plus légère que les autres. Trouver en n+2 pesées cette fausse pièce et préciser si elle est plus lourde ou plus légère.

SOLUTION

Nous allons faire une preuve par récurrence sur n
Considérons deux types de situations Pn et Qn :
Situation Pn : un tas T de 4x3ⁿ pièces en apparence identiques dont l'une est fausse , ou plus lourde ou plus légère que les autres ;
Situation Qn : deux tas U et V de 4x3ⁿ pièces, en apparence identiques dont une appartenant à U est plus lourde ou (exclusif) une appartenant à V est plus légère que les autres.

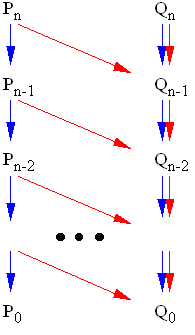
-Nous savons résoudre le problème pour Po et Qo en deux pesées. -En une pesée nous pouvons passer de la situation Pn à la situation Pn-1 ou Qn-1.       En effet, partageons Pn en trois tas ayant le même nombre de pièces       et comparons deux tas : un sur chaque plateau.       S'il y a équilibre nous sommes en Pn-1 (flèche bleue) avec le tas restant       sinon en Qn-1 (flèche rouge) avec les deux tas comparés. -En une pesée nous pouvons passer de la situation Qn à la situation Qn-1.       En effet, partageons le tas U       en trois tas U1, U2 et U3 ayant le même nombre de pièces et partageons       le tas V en trois tas V1, V2 et V3 ayant le même nombre de pièces.       Comparons alors (U1 et V2) avec (V1 et U2).       S'il y a équilibre nous sommes en Qn-1 (flèche bleue)  avec les tas U3 et V3       sinon en Qn-1 (flèche rouge) avec les tas (U1 et V1) ou (U2 et V2) selon le       sens du déséquilibre de la balance. La récurrence est donc résolue à partir de Pn. Remarque Une pesée ayant trois issues partage l'ensemble des possibles en trois cas. Deux pesées partagent l'ensemble de départ en neuf cas. Trois pesées partagent l'ensemble de départ en 33 = 27 cas, etc. Dans les 12 pièces, chaque pièce pouvant être ou plus lourde ou plus légère nous avons 24 possibilités de solutions.

S'il n'est pas possible d'isoler chaque élément en deux pesées on peut y arriver en trois pesées car 24 < 3³.