"Nul n'entre ici s'il n'est géomètre"
écrit selon la légende sur le fronton de l'Académie de Platon
.
|
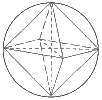
Un polyèdre régulier est inscriptible dans une sphère et toutes ses faces sont des polygones réguliers isométriques (Un polygone régulier a tous ses côtés isométriques et tous ses angles sont de même mesure).
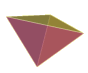
Euclide termina son œuvre Les Eléments en prouvant qu'il existe exactement 5 polyèdres convexes réguliers : le tétraèdre, le cube, l'octaèdre, le dodécaèdre et l'icosaèdre.
Ces solides sont appelés communément solides de Platon car ce dernier les a décrits dans le Timée, vers 350 av. J.-C. Il a été séduit par leur beauté et leur symétrie. Les grecs ont accordé une signification mystique aux cinq solides réguliers en les rattachant aux grandes entités qui selon eux façonnaient le monde : le Feu est associé au tétraèdre, l'Air à l'octaèdre, la Terre au cube, l'Univers au dodécaèdre et l'Eau à l'icosaèdre.
Pythagore de Samos (environ 550 av. J.-C.), a probablement connu trois de ces solides : le cube, le tétraèdre et le dodécaèdre.
A la Renaissance Kepler (1571-1630) pensait que le nombre et la disposition des planètes était une manifestation de la volonté de Dieu et n'était donc pas arbitraire. Il encastra les 6 planètes connues à l'époque dans les 5 solides parfaits platoniciens.
A chaque sphère est associée une planète, le rayon de la sphère donne la distance moyenne de la planète au soleil. Chaque polyèdre est inscrit dans une sphère et circonscrit dans une autre.
Vénus correspondait à l'octaèdre, la Terre à l'icosaèdre, Mars au Dodécaèdre, Jupiter au tétraèdre et Saturne au cube.
Nous pouvons vérifier pour chaque solide de Platon la formule d'Euler obtenue avec le nombre F de faces, A d'arêtes et S de sommets :
F+S=A+2
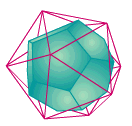
DUALd'un polyèdre :
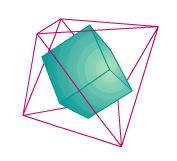
on appelle polyèdre dual d'un polyèdre régulier P le polyèdre P' dont les sommets sont les centres des faces du polyèdre P. Si P' est le dual de P, alors le dual de P' est semblable à P. Ainsi le dual d'un cube est un octaèdre régulier et réciproquement.
Tétraèdre Cube Octaèdre Dodécaèdre Icosaèdre
SOLIDES ETOILES
Quelques exemples.
Ces exemples ne sont pas encore pris en charge par Ruffle.
Je les replacerai dès qu'il seront exécutables avec Ruffle ...
L'icosaèdre
Il est composé de 20 faces qui sont des triangles équilatéraux.
Il a 12 sommets et 30 arêtes. Il a 5 arêtes en chacun des
sommets. Chez les grecs, il était le symbole de l'eau.
 |
| Le
dual de l'icosaèdre est le dodécaèdre composé de 12 faces et de 20 sommets. |
 |
Dôme géodésique de l'Exposition universelle de 1967 qui a eu lieu à Montréal (Canada)
construit d'après les plans de Richard Buckminster Fuller (1895-1983).
Ce pavillon a été depuis transformé en un musée consacré à l'eau et à l'environnement.
C'est une structure sphérique constituée de grands cercles géodésiques
qui se croisent en formant des triangles qui en assurent la rigidité.
Ce modèle comprend un icosaèdre inscrit dans une sphère.
Chaque face est divisée en un réseau de triangles projetés sur la sphère.
Cette structure légère rigide facile à monter présente de nombreux avantages.
C'est un grand espace libre rigide, dont le rapport entre volume intérieur maximal et surface extérieure minimale est optimal pour le chauffage.
Il est composé de 12 faces qui sont des pentagones réguliers.
Il a 20 sommets et 30 arêtes. Il a 3 arêtes en chacun des
sommets.
Chez les grecs, il était le symbole de l'Univers.
ICI
le dodécaèdre dynamique en dimension 3
CLIQUER
Le dual du dodécaèdre est l'icosaèdre
composé de 20 faces et de 12 sommets.
L'octaèdre
Tous les autres patrons ici.
Il est composé de 8 faces qui sont des triangles équilatéraux.
Il a 6 sommets et 12 arêtes. Il a 4 arêtes en chacun des sommets.
Chez les grecs, il était le symbole de l'air.
ICI
l'octaèdre dynamique en dimension 3
 |
| Le
dual de l'octaèdre est le cube composé de 6 faces et de 8 sommets. |
 |
Sculpture de Québec
sur la la terrasse Dufferin,
dominant le cap Diamant,
dans la Haute-Ville de Québec.
Elle rappelle que le Canada
est le troisième producteur
de diamants au monde
par la valeur de sa production,
après le Botswana et la Russie.
C'est un octaèdre régulier (le diamant)
dans une sphère (le monde).
