Analyse
et SOLUTION
Ce problème
est un paradoxe surprenant. Et il révèle que certaines
informations paraissant utiles ne le sont pas du tout.
Ce travers est souvent utilisé par les maisons de jeux...
Comme les cartes tirées ne sont pas cachées, on est
informé des couleurs qui restent dans le paquet.
On pense assez naturellement que cette information ne peut être
qu'utile.
Mais cette information ne nous donne rien !
NON, on ne peut pas espérer gagner plus d'une fois sur deux
statistiquement.
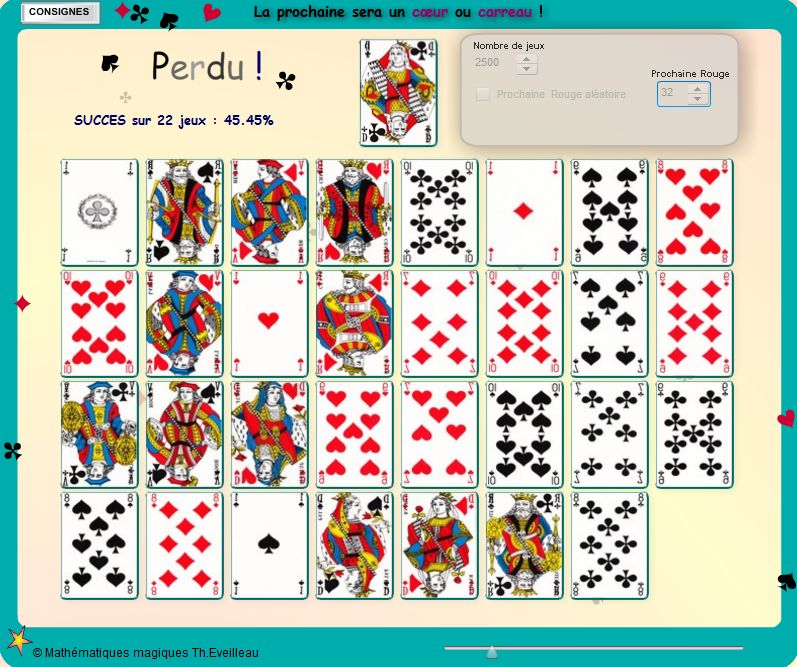
D'ailleurs les résultats de l'animation, sur de nombreux
jeux le confirment : la moyenne obtenue tourne autour de 50%.
Mathématiquement l'espérance est de 50%, une
chance sur deux, ni plus ni moins
et ce quelle que soit le rang de la carte prochaine choisie.
Inutile donc de chercher une stratégie plus performante qu'une
autre. Il n'y en a pas.
ANALYSE
-
Parions dès la première carte : "Elle sera
rouge ! ".
C'est évident on a une chance sur deux de gagner.
- Parions sur la dernière carte :
"Elle sera rouge ! ".
Nous savons exactement quelle sera sa couleur car nous voyons toutes
les cartes déjà sorties.
Si elle est rouge, c'est OK, nous avons gagné.
Mais si on sait qu'elle doit être noire, nous perdons car
nous ne pouvons pas dire qu'elle sera noire.
On doit dire: "Elle sera
rouge ! ".
C'est la règle du jeu ! Donc nous perdons et finalement même
dans ce cas, nous n'avons qu'une chance sur deux de gagner.
Imaginons que nous ayons choisi une stratégie : une position
après avoir vu défiler des cartes.
Par
exemple la position n pour la prochaine carte qui devra être
rouge.
Nous avons (n - 1) cartes avant et (32 - n) cartes ensuite.
Le
nombre de possibilités (de rangements des cartes) où
la carte n° (n-1) est suivie d'une carte ROUGE,
donc gagnante est le même que le nombre de possibilités
où cette carte est suivie d'une carte NOIRE.
Ceci car les
couleurs NOIRE
et ROUGE
ont un rôle symétrique
dans le jeu.
Nous avons autant de dispositions c1, c2,
c3,... cn-1, cn,
cn+1,... c32 avec la
nième carte ROUGE
que de dispositions c1, c2,
c3,... cn-1, cn,
cn+1,... c32 avec la
nième carte NOIRE.
Si
l'on regarde les 32 ! =1*2*3*...*32
dispositions possibles des cartes, on peut les classer en deux paquets
de 32 ! / 2 cartes, correspondant aux deux dispositions précédentes
selon la couleur de la nième carte.
Ceci
est valable
- quel que soit le rang n choisi pour désigner la prochaine
carte qui sera rouge et
- quelles que soient les (n-1) premières cartes sorties.
Ainsi, l'information donnée par les cartes visibles n'est
pas utile.
On
peut vérifier que la moyenne du nombre de succès,
donnée par l'animation ci-dessus, 'tourne' autour de 50%
dès que le nombre de jeux est important.