Le problème

Nous savons que la quadrature du cercle est IMPOSSIBLE : on ne peut pas construire rigoureusement à la règle et au compas, un carré dont l'aire est exactement celle du cercle. Cependant, nous pouvons construire un rectangle à partir d'une partie du disque. Comment découper l'intérieur non coloré en noir, du disque ci-contre, pour ensuite réassembler les morceaux en un rectangle ? Il faudra donner les dimensions du rectangle reconstitué. A partir de là, il sera facile de calculer l'aire de la partie du disque constituée des trois petites rosaces noires.

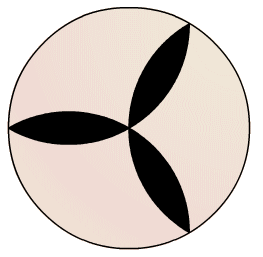ANIMATION

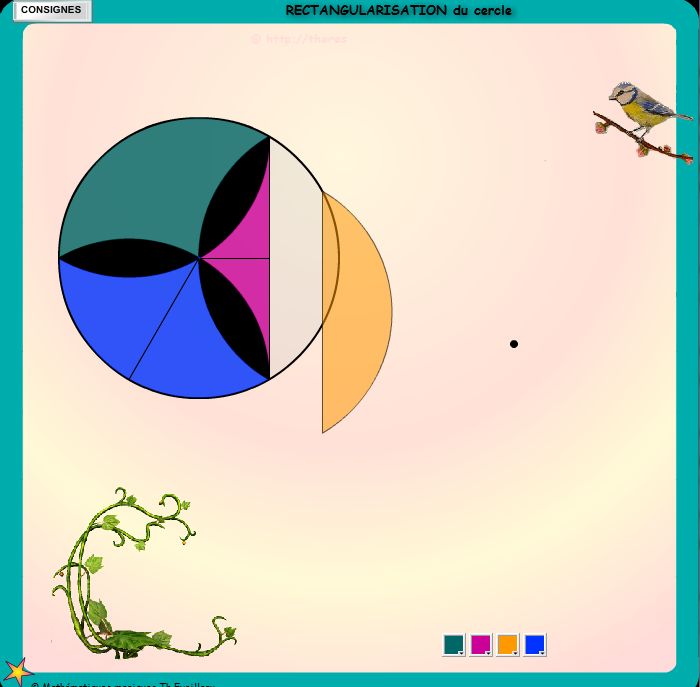
Cette animation donne le découpage du disque.

Il s'agit de déplacer les 6 pièces colorées pour obtenir un rectangle.
Le point noir de la partie droite indique le centre du rectangle à reconstituer avec les morceaux colorés.
Pour le contrôle du jeu, le rectangle a les côtés parallèles au cadre de l'animation.

Les déplacements peuvent être effectués avec la SOURIS ou bien avec les flèches du CLAVIER :
    - GAUCHE et DROITE pour déplacer une pièce vers la gauche ou vers la droite.
    - HAUT et BAS pour déplacer une pièce vers le haut ou le bas du cadre.

Les rotations d'une pièce s'effectuent soit avec
    - la BARRE d'ESPACE pour tourner dans le sens horaire ;
    - la TOUCHE CONTROL (CRTL) pour tourner dans le sens anti-horaire.



Le bouton RAZ permet de tout réinitialiser.

  CLIQUER

    

SOLUTION


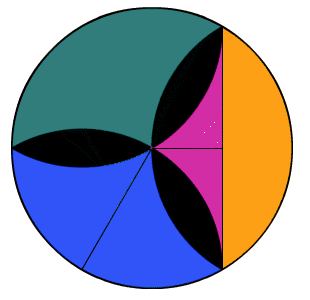
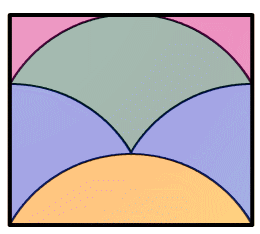
Prenons un cercle de rayon unité 1.

On découpe comme indiqué ci-contre le cercle en six nouveaux morceaux qui permettent de reconstituer le rectangle ci-après. La longueur du rectangle, soit le segment de base du secteur jaune a pour longueur deux fois la hauteur d'un triangle demi-équilatéral de côté le rayon du cercle donc l'unté. Cette longueur vaut donc 2 * / 2 = La largeur du rectangle est 1 + 1/2 = 3/2 (1/2 venant du demi-côté du triangle équilatéral précédent).

Comme le cercle est de rayon 1, son aire π R² = π .
et l'aire des trois rosaces est :
π -3 * /2 ~ 0.5435

RETOUR