Le problème
La construction animée
Aire et périmètre
Reuleaux entre deux parallèles PUIS dans un carré
Le projecteur d'images
Le moteur Wankel
Autres applications
L'épitrochoïde amusez-vous !
Et la cycloïde
Une bien jolie couverture
Le
problème
Percer
des trous carrés est un défi.
Est-il possible de faire des trous carrés dans une plaque avec
une perceuse spéciale ?
Existe-t-il
un appareil qui en générant une rotation continue autour
d’un axe permette une projection nette d'images ?
Chaque image doit rester un moment immobile, tandis que la transition
d’une image à l’autre doit se dérouler dans
un temps beaucoup plus court.
SOLUTION
|
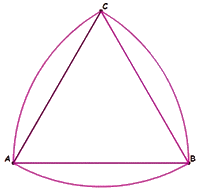
La
solution est obtenue à l'aide d'un
triangle de Reuleaux, du
nom de son concepteur Franz Reuleaux ingénieur
allemand (1829-1905). On
part d'un triangle équilatéral complété
par |
|

|
On trouve mention de ce triangle dans les travaux de Léonard de Vinci (ci-contre à gauche), ou dans les fenêtres de la cathédrale Saint-Sauveur de Bruges (ci-contre à droite). Leonhard Euler (1707-1783) a étudié ces formes qu’il nommait «orbiforme ». |

|
Périmètre
et aire du triangle de Reuleaux
Si
R est le côté du triangle équilatéral tracé
dans le Reuleaux,
on voit
que le périmètre du
Reuleaux est égal à la moitié
du périmètre du cercle de rayon R
(nous avons trois arcs de 1/6ème de tour : chacun de 60°).
L'aire est égale
à celle de trois sixièmes d'un disque de rayon R, moins
deux fois celle du triangle équilatéral.
Nous trouvons donc une aire de 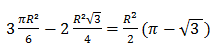 .
.
Cette aire est
de façon évidente plus petite que celle du
disque de rayon R qui
est de πR².
La construction d'un triangle de Reuleaux est ainsi plus
économique en matière première que
celle d'un disque de même diamètre.
Dans les trois animations qui suivent, ne pas hésiter à modifier les couleurs avec les boutons couleur du bas de chaque écran.
Voici
pas à pas, la construction animée de ce triangle.
Utiliser les boutons
fléchés pour faire avancer l'animation.
Moduler éventuellement la vitesse avec le curseur en bas de l'animation.
On peut utiliser le mode MANUEL ou bien AUTOmatique avec les boutons adéquats.
Les gros points sont manipulables lorsqu'ils sont visibles en mode MANUEL.
CLIQUER
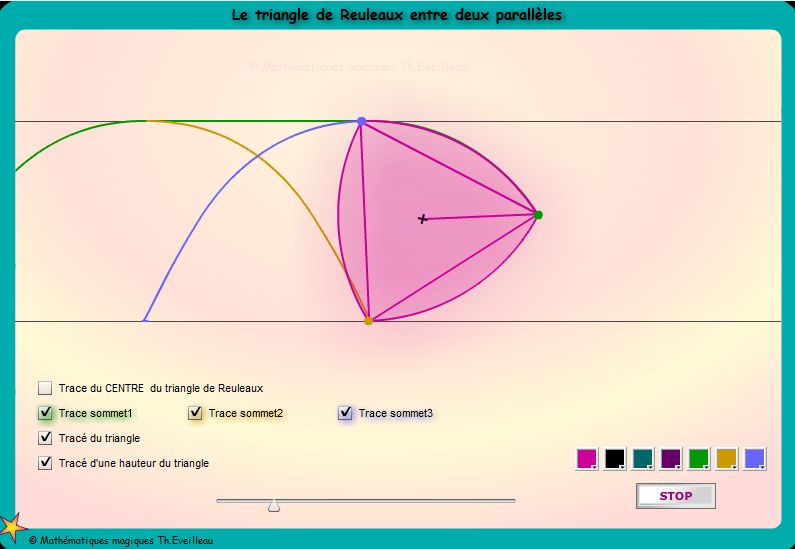
Le
triangle de Reuleaux roule entre deux parallèles ET tourne dans
un carré.
Une particularité de
cet objet est que sa largeur est constante.
On parle de diamètre constant quelle que soit son orientation.
Ce diamètre est égal au côté du triangle équilatéral
de base ayant servi à sa construction.
Une propriété importante d'un triangle de Reuleaux apparaît
: on peut le faire rouler entre deux
parallèles.
Dans ce cas le centre de gravité du triangle de Reuleaux décrit
une courbe périodique.
Les sommets du triangle décrivent une cycloïde, lieu d'un
point d'un cercle qui roule sans glisser sur une droite
Cf la cycloïde à la fin de ce document.
CLIQUER
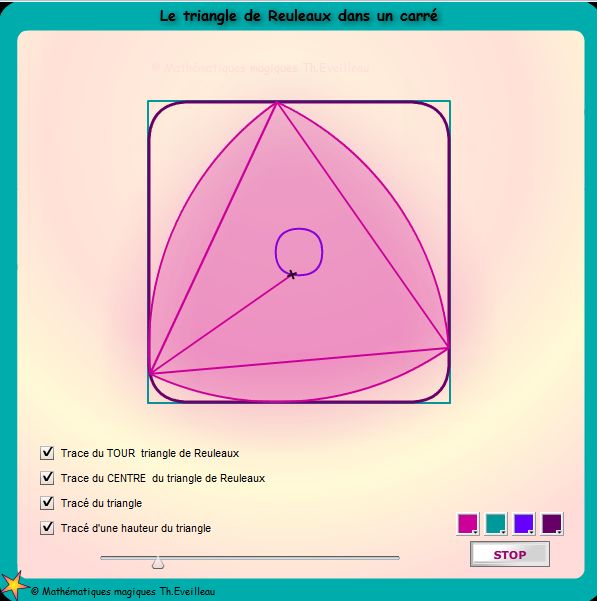
MIEUX encore : on peut le faire tourner dans un carré.
En tournant sur lui-même, il trace un carré à bords arrondis (elliptiques).
Une conséquence pratique est la possibilité de construire une perceuse qui pourra fabriquer des trous presque carrés.
L'usure en fera un carré parfait...
Dans l'animation suivante, cliquer le bouton TOURNER pour lancer la rotation du triangle de Reuleaux.
On peut ensuite la stopper avec le bouton STOP.
Ensuite demander les différentes TRACES proposées et notamment celles des sommets du Reuleaux pour voir la trace presque carrée,
que laissera ce triangle.
Moduler éventuellement la vitesse avec le curseur en bas de l'animation.
Voici
une perceuse utilisant le principe précédent. Pour faire tourner le triangle, l'articulation est réalisée avec un joint de Cardan (de son inventeur Jérôme Cardan (1501-1576). Cette articulation est utilisée également pour relier une remorque à un camion. Les coins obtenus sont légèrement arrondis, en prolongeant les côtés on obtient un carré parfait. |

|
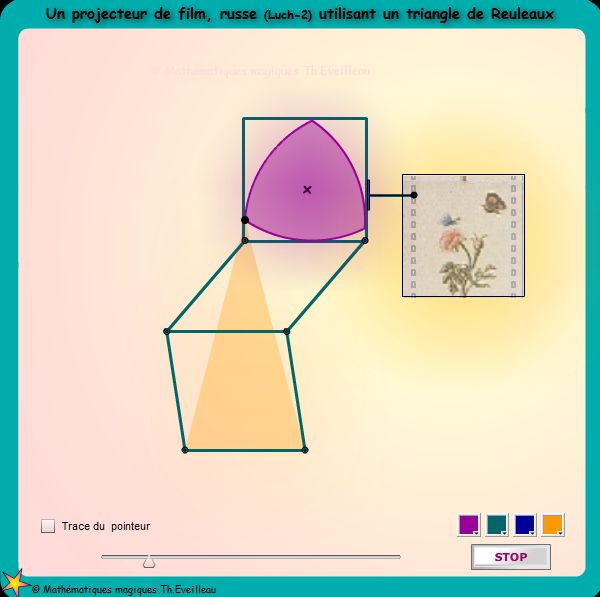
Une
application : le projecteur d'images, russe (Luch-2) utilisant un triangle
de Reuleaux
Dans ce projecteur,
l'image reste visible et immobile pendant les 5/6èmes d'un tour
et la transition dure 1/6ème de tour.
Cette fois le triangle de Reuleaux tourne autour d'un de ses sommets.
Il reste toujours à l'intérieur d'un carré dont le
centre n'est pas fixe.
Ce centre parcourt un carré, à bords arrondis, superposable
à celui décrit par le pointeur (le pointeur
est un point translaté du centre du carré).
Moduler éventuellement la vitesse avec le curseur en bas de l'animation.
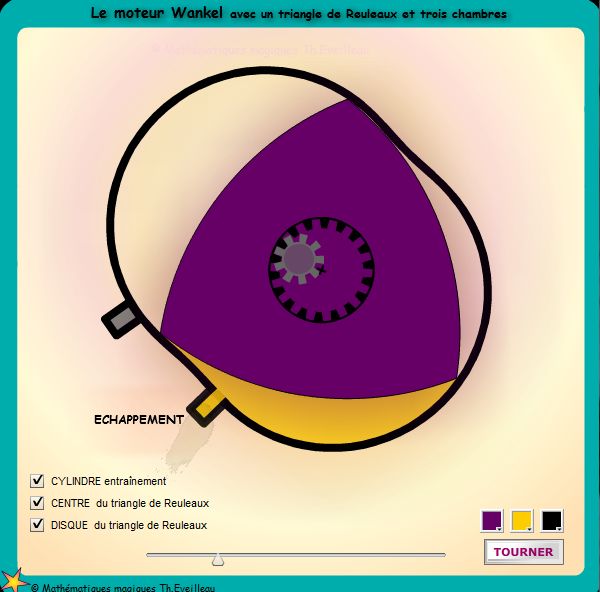
Dans
l'industrie : le moteur Wankel
C'est un moteur à piston rotatif inventé
par Félix Wankel autour de 1950.
Il utilise trois chambres de combustion dont les volumes varient
avec la rotation du triangle de Reuleaux, à l'intérieur
d'une pièce dont la forme est définie mathématiquement
par une épitrochoïde.
On retrouve les différentes étapes d'un moteur à
quatre temps : admission, compression, allumage et explosion quand la
compression est maximale puis échappement.
Ce moteur
fonctionne avec un mélange d'air et d'essence.
Il est arrivé sur le marché au moment du premier choc pétrolier
en 1973, et n'a malheureusement pu combler son manque d'expérience
face à des moteurs classiques.
Son concept est séduisant et efrficace, il est aussi silencieux,
mais sa consommation est excessive.
Aussi Citroën puis Peugeot ont abandonné les recherches sur
ce moteur.
Pourtant la Mazda 787B a remporté les
24 heures du Mans avec un prototype Wankel qui a été interdit
sous la pression d'autres constructeurs.
Pourquoi les plaques d'égout sont-elles presque toujours rondes ?
|
Cela provient d'une propriété mathématique : une largeur constante empêche la plaque d'égout de tomber accidentellement dans le trou.
Plus généralement,
|
  |
|
|
|
Tout comme il existe des triangles de diamètre constant, il existe d'autres polygones réguliers ayant cette propriété.
Ceux ayant un nombre impair de côtés : pentagones, heptagones, etc. peuvent avoir un diamètre constant.
Des pièces de monnaie utilisent aussi ce triangle courbe (pratique pour la reconnaissance dans un distributeur automatique).
Par exemple, la pièce de 50 pence anglaise est un heptagone de Reuleaux.

Si l'on juxtapose
plusieurs triangles de Reuleaux, la distance entre leurs centres reste
constante.
On peut alors les faire tourner l'un sur l'autre...
Les possibilités d'utilisation sont nombreuses.
La
courbe mathématique qui se cache derrière le triangle de
Reuleaux
L'épitrochoïde
est une courbe plane, correspondant à la trajectoire d'un point
fixé à un cercle mobile qui roule sans glisser sur et autour
d'un autre cercle dit directeur.
Observer l'évolution de l'épitrochoïde
dans l'animation suivante.
Suivre son évolution quand les paramètres
changent : rayons des cercles Fixe et Tournant, position du point à
tracer (angle et rapport au rayon), et enfin le rapport dans les angles
de rotation.
Ne pas hésiter à modifier les couleurs au cours du tracé.
Essayer de trouver la courbe correspondant au moteur Wankel.
Et la cycloïde entre les deux parallèles
Où l'on retrouve
maintenant la valve d'une roue.
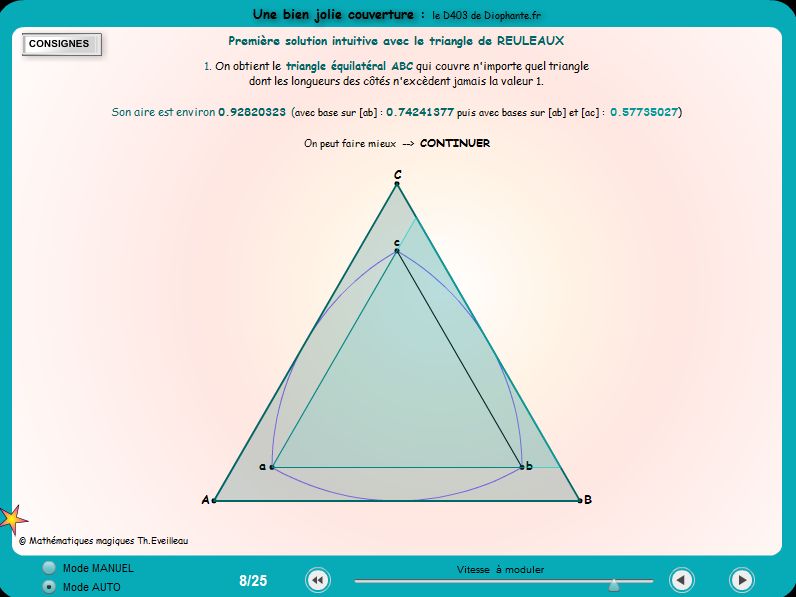
Il s'agit du
casse-tête D403 de Diophante.fr Novembre
2017 :
Trouver le triangle d'aire minimale qui couvre n'importe quel triangle
dont les longueurs des côtés n'excèdent jamais la
valeur 1.
L'animation suivante prmet de comprendre comment petit à petit
on trouve et essaie d'améliorer une solution.
 |
Pour
en savoir plus : https://fr.wikipedia.org/wiki/%C3%89pitrocho%C3%AFde
Ici une vidéo
avec une bicyclette dont les roues sont des triangles de Reuleaux :
https://www.youtube.com/watch?v=BeOS9pG6vjU&feature=youtu.be
Et d'autres explications ici :
https://www.youtube.com/watch?v=quuw4HC96bE