La rumeur Le bruit court que... Elle court, Elle court la rumeur...   Ce thème a été imaginé pour faire comprendre la notion de modèle et m'a été proposé par Pierre Jullien. Le modèle est purement pédagogique. Cependant il ouvre la porte à une certaine spéculation sur la réalité du monde. Il n'est peut-être pas aussi abstrait qu'il y paraît. Soit une population de N individus. Un jour l'un d'entre eux possède une nouvelle extraordinaire et s'empresse de la propager, en la divulguant à tous ceux qu'il rencontre et ceux-ci la propagent à leur tour. Cependant lorsque quelqu'un qui connaît la nouvelle l'annonce à quelqu'un qui la connaît déjà, il s'imagine que tout le monde la connaît et s'arrête de la propager et l'autre aussi. Que va-t-il se passer lorsque deux individus A et B se rencontrent ?   La rumeur chez les voisins Non, c'est vrai ! ?... Comme, je vous le dis ! 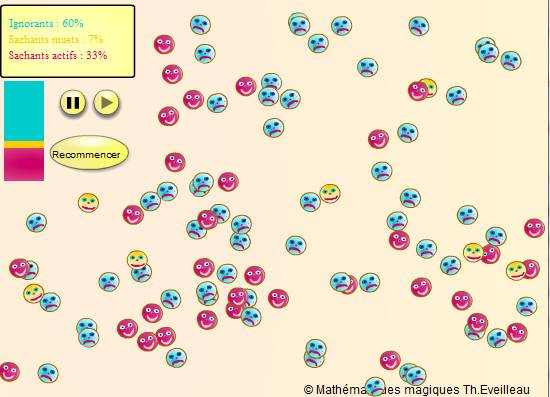Ci-dessous, la rumeur se propage de bouche à oreille. Chacun peut raconter la nouvelle à son voisin. Nous allons constater que la rumeur s'arrête assez rapidement puisqu'elle est liée à la position géographique des voisins. Choisir le nombre de personnes et de sachants au départ à l'aide des flèches. Ensuite cliquer GO.. CLIQUER Et ce bruit qui court Est un fait qui nous dépasse Duquel on se défend toujours Mais, bref, où tous, ON y passe... EsteBan Hache le 13.07.2003 à 1h30 La rumeur téléphonique chez le ON... A fait-ci, a fait ca, a été mélé... A ce que l'ON m'a dit ! Ci-dessous, la rumeur se propage par téléphone et n'est plus liée à la géographie des lieux. Les appels téléphoniques ont lieu de manière aléatoire équiprobable. Chacun peut raconter la nouvelle à son interlocuteur. Cette fois la rumeur se propage pendant une durée plus longue. CLIQUER Cette atteinte, d'irresponsable Peut faire couler bien des sangs... ANALYSE Le tableau ci-dessous précise ce qui se passe lors des différentes rencontres.   B sachant actif B sachant muet B ignorant A sachant actif A devient muet B devient muet A devient muet B reste muet A reste actif B reste actif A sachant muet A reste muet B devient muet A reste muet B reste muet A reste muet B reste ignorant A ignorant A devient actif B reste actif A reste ignorant B reste muet A reste ignorant B reste ignorant En notant A le nombre de sachants actifs, M le nombre de sachants muets et I le nombre d'ignorants, au début on a (A, M, I) = (1, 0, N-1). 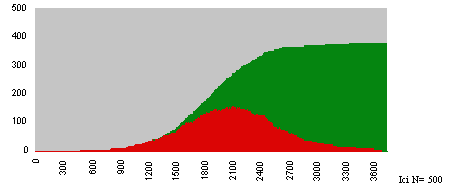A partir de là, les rencontres ont lieu une par une à un rythme uniforme, de manière aléatoire équiprobable. On peut représenter l'évolution du système par un graphique, où le temps est porté en abscisse, en portant en ordonnée A et A+M. C'est-à-dire l'effectif des sachants actifs et celui M de tous les sachants muets. L'effectif des ignorants est donc N-S. Au début A reste égal à 1 car l'individu qui connaît la nouvelle n'est pas encore impliqué dans les rencontres. Puis apparaissent de nouveaux sachants actifs... jusqu'à ce que deux d'entre eux se rencontrent et deviennent muets. Le nombre A des sachants actifs croît et celui M des muets aussi. Puis A atteint un maximum et décroît (avec quelques soubresauts) pour inexorablement s'annuler. La rumeur ne se propage plus. Un certain nombre d'ignorants subsiste. A chacun de faire ses simulations et statistiques...