Un triangle équilatéral ABC est incrit dans un cercle. Le point D se déplace sur le cercle donné. Quelle relation lie les trois segments [CD], [BD] et [AD] ?

SOLUTION

La longueur du segment le plus long est toujours égale à la somme des longueurs des deux autres.

En effet, nous avons ce beau résultat :
Théorème de Ptolémée — Un quadrilatère convexe est inscriptible si et seulement si le produit des longueurs des diagonales est égal à la somme des produits des longueurs des côtés opposés.

Le triangle ABC est équilatéral donc AB=BC=CA.
Posons a =AB=BC=CA.

Selon la position du point D sur le cercle, la diagonale du quadrilatère inscrit dans le cercle va changer.
.Si c'est [CD], alors CD*AB = BD*CA + DA*BC c'est à dire : CD*a = BD*a + DA*a d'où CD = BD + DA
.Si c'est [BD], alors BD*AC = CD*AB + DA*BC c'est à dire : BD*a = CD*a + DA*a d'où BD = CD+ DA
.Si c'est [DA ], alors DA*BC = CD*AB + BD*AC c'est à dire : DA*a = CD*a + BD*a d'où DA = CD + BD

ANIMATION

L'animation suivante explicite les différentes longueurs des trois segments [CD], [BD] et [DA ].


On peut déplacer les points A et/ou D en mode MANUEL en cliquant le bouton STOP.
Pour cela utiliser soit la souris ou bien les quatre flèches du CLAVIER.
Elles permettent de déplacer sur le cercle le dernier point sélectionné avec la souris.

Relancer ensuite l'animation avec le bouton TOURNER.

CLIQUER

 

 

Autre SOLUTION de Pierre Jullien

Sur le cercle, le segment CE se déduit de AD par rotation d'un tiers de tour dans le sens des aiguilles d'une montre.


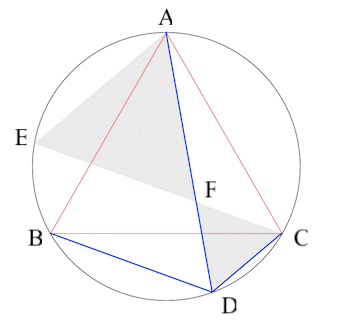
Les triangles AEF et CFD sont équilatéraux.
FA = FE = DB et DF = DC
Ainsi DA = DF + FA = DC + DB.