|
Visualiser
la somme des carrés des entiers
Nombres pyramidaux
 La
somme des carrés des entiers
Constituons
un pyramidal en empilant quatre étages carrés.
Nous avons un carré de 1 case, puis un carré de 2²
= 4 cases,
puis de 3² = 9 cases et enfin de 4² = 16 cases.
CLIQUER
Le déplacement
de la souris modifie la direction du mouvement.
Cliquer le pyramidal pour stopper le mouvement.
Recliquer pour redémarrer.
Maintenant, comme
dans un puzzle 3D, agençons six pyramidaux pour reconstituer
un parallélépipède rectangle de dimensions
4, 5 et (2 x 4 + 1 =) 9.
Nous obtenons alors :
|
12
+ 22 + 32 + 42 = (
4 x 5 x 9 ) / 6
|
CLIQUER
|
De
même agençons six pyramidaux constitués
de carrés de 1 à 5² cases.
Nous obtenons un parallélépipède
de
dimensions 5, 6 et (2 x
5 + 1 =) 11.
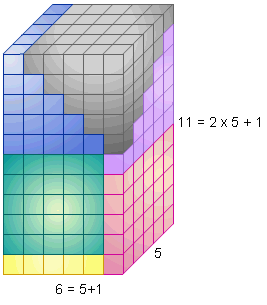
Somme des carrés des 5 premiers entiers
|
12
+ 22 + 32 + 42
+
52 = (
5 x 6 x 11 ) / 6
|
|
Somme des carrés des 6 premiers entiers
|
12
+ 22 + 32 + 42
+ 52 +
62= (
6 x 7 x 13 ) / 6
|
|
|
Le procédé se généralise avec un pyramidal
obtenu en empilant des carrés de 1 à n² cases.
Six pyramidaux réunis permettent de construire un parallélépipède
de dimensions n, n+1 et 2n+1.
Nous obtenons le résultat général :
|
12
+ 22 + 32 + 42 + 52
+ 62 + 72 +... + n2 = n (n+1)
(2n+1) / 6
|
L'idée
des pyramidaux figure dans le 4ème tome des Récréations
mathématiques
d'Edouard Lucas, publié en 1894 (réédité chez Blanchard).
Voici quelques extraits de cet ouvrage.
|
