Un
triangle pour un spaghetti coupé en trois
?
Le
problème
On coupe au hasard un spaghetti en trois parties.
Quelle est la probabilité de pouvoir réaliser un triangle
avec les 3 morceaux obtenus ?
Modélisation
Méthode
choisie :
on détermine de façon aléatoire deux points sur
le spaghetti et on coupe.
Les trois morceaux ainsi obtenus sont de longueur parfaitement aléatoire.
Pour
des raisons pratiques d'affichage, seules deux décimales des
longueurs sont affichées.
Cependant, elles sont toutes calculées dans le tirage et effectives
dans le tracé.
On
peut visualiser
- la construction pas à pas des triangles OU bien visualiser
- les points de coordonnées x et y correspondant aux coupes.
Les points sont verts quand le triangle
est constructible, rose foncé quand
ce n'est pas possible.
50 000
points donnent une bonne représentation.
*ATTENTION à bien appuyer
la touche ENTREE pour valider le nombre, si l'on choisit d'écrire
le nombre d'expériences avec le clavier.
CLIQUER

ANALYSE
Choisissons
comme unité de mesure la longueur du spaghetti.
On obtient ainsi simultanément trois morceaux de longueurs
respectives x, y et z.
Si
z est le plus grand des côtés alors pour que le triangle
soit constructible,
il faut avoir l'inégalité triangulaire : z < x +
y.
Par ailleurs,
x < z donc x < y + z.
De même ,
y < z et donc y < x + z.
Par symétrie et ce quel que soit le plus grand côté,
pour obtenir un triangle (non aplati),
les inégalités triangulaires suivantes, doivent être
vérifiées simultanément :
x
< y + z ,
y < x + z ,
z < x + y.
On a :
z = 1 - x - y
et les inégalités ci-dessus conduisent à :
x < y + z , soit x < y + 1 - x - y ou 2x < 1 et x
< 1/2.
Et par symétrie :
x < 1/2
et z < 1/2.
FINALEMENT
:
x > 0,
y > 0
1 - x -
y > 0
donnent l'ensemble des possibilités.
Et
:
x < 1/2
y <
1/2
x + y >
1/2
donnent l'ensemble des cas favorables.
Nous obtenons un problème de régionnement du
plan.
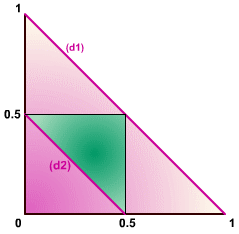
Dans le repère (Ox, Oy), traçons les droites
(d1) d'équation : x +
y = 1 soit y = 1 -
x,
et
(d2) d'équation : x +
y = 1/2 soit y = 1/2 - x.
La probabilité se traduit par les aires : p = 1/4 soit
25%.
L'aire verte correspondant aux cas favorables, l'aire totale
(cas possibles) correspondant
au demi-carré de côté 1. |
|