Explications
et résultats
La recherche du surplomb
maximum avec des briques, des dominos ou des sucres est un subtil
problème d'équilibre.
Nous allons d'abord essayer de comprendre comment deux briques peuvent
tenir l'une sur l'autre, puis trois...
On suppose que toutes les briques sont identiques.
Soit d la largeur d'une brique ; h
la hauteur de chaque brique, et enfin m
sa masse.
La brique N° n : Bn
possède un centre de gravité Gn
en son milieu. Son abscisse st donc xn.
Cette brique possède un surplomb de dn
par rapport à la brique Bn-1 qui
est au-dessous.
Dans le cas de
- deux briques, le surplomb est maximal si la brique du dessus dépasse
de d/2 la brique du dessous.
Exemple avec une brique de largeur 200
:

- trois briques, le raisonnement est identique, mais nous devons tenir
compte de la masse des deux briques du dessus.
Le centre de gravité de l'ensemble des deux dominos du dessus
(situé à la distance 0.75* d
de la gauche, soit ici 150 du bord gauche,
ne doit pas dépasser de d/2 le bord
gauche de la brique du bas.
Position maximale en prenant le résultat
précédent pour les briques du dessus :

Le centre
de gravité de ces trois briques est maintenant celui des deux
briques vertes (masse 2m) et de celui de
la brique grise du bas de masse m.
Il est situé à (d/2)/3 = d/6 du
bord gauche de la base de ce bloc de 3 briques.
Le centre de gravité
a pour position extrême le bord gauche de la brique du socle.
Ceci donne un surplomb de :
0.5*d + 0.25*d + d/6 = 11/12 *d
Ainsi pour une brique de largeur 200, on obtient avec ces 3 briques
un surplomb de 183.3 ... approchant déjà
la largeur d'une brique !
Dans
l'animation je mesure les déplacements à 0.05 pixel
près.
Equilibre à exactement 108+1/3 :

Déséquilibre à 183.35 :

Avec 4 briques, nous dépassons la largeur d'une brique !
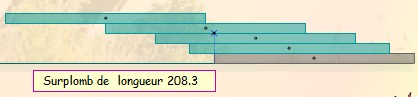
C'est exactement 208 + 1/3.
0.5*d + 0.25*d + d/6 + d/8 = 25/24 *d
Autres exemples de résultats obtenus :


Rien ne sert de courir vite au départ... il faut démarrer
doucement...
On pourrait faire légèrement mieux en théorie
avec 385.44... pour 26 briques.
La différence est due à la précision choisie
dans l'affichage : à 0.05 pixel près.
Impossible physiquement de faire mieux.
Cela diminue légèrement l'optimalité à
chaque étage.
Pour
une brique de longueur égale à l'unité
Nous avons
avec 3 briques, à la limite du basculement, un surplomb de
:
1/2 +1/4 +1/6 ;
Avec 4 briques, le surplomb dépasse 1, car 1/2
+ 1/4 + 1/6 + 1/8 = 1,041 ;
.
.
Avec 31
briques, il dépasse 2.
Pour un surplomb plus grand que 3,
il faut 227
briques.
Pour un surplomb de plus de 10,
il faut disposer soigneusement 272
400 600 briques
Et ainsi de suite... on obtient la "série harmonique"
qui tend vers l'infini mais... très lentement :
1/2 + 1/4 + 1/6 + ... + 1/(2n) =
1/2 (1 + 1/2 + 1/3 + ... + 1/n)
Ce qui est extraordinaire est qu'avec cette méthode
on peut obtenir un surplomb aussi grand que l'on veut.
MAIS il faudra peut-être utiliser une quantité énorme
de briques.
On choisit de décaler la brique la plus élevée
de la moitié de sa longueur par rapport à celle qui
est juste en dessous.
Cette dernière est décalée de 1/4 de sa longueur
par rapport à la précédente, elle-même
décalée de 1/6, etc.
Bien sûr,
cet empilement est dans un équilibre peu stable.
Il suffit de diminuer très légèrement le surplomb
à chaque étage pour augmenter la stabilité de
l'édifice.
Le
paradoxe du surplomb infini
La somme
des n premiers termes de cette série nommée harmonique,
1 + 1/2 + 1/3 + ... ,
- vaut à peu près ln(n)
: le logarithme de n
- tend, lentement, mais c'est certain, vers l'infini.
La
formule suivante nous donne une idée du résultat
pour un très grand nombre de briques.
Nous utilisons la constante dite d'Euler Mascheroni :

De façon générale,
avec un très nombre n de briques dont chacune a une longueur
de Lg,
le surplomb maximal est d'environ : 0.5
* Lg * Ln(n) +0.577215
On trouve ici avec 1000 briques dont chacune mesure 200 unités,
un surplomd maximal d'environ :
0.5*200*Ln(1000)+0.577215 ~ 748.497
|
Cf
http://mathworld.wolfram.com/HarmonicSeries.html
ou
https://www.math.dartmouth.edu//~pw/papers/sodaproc2.pdf
En prenant assez de briques, le sommet d'une pile se trouve donc en
surplomb d'une longueur aussi grande qu'on le désire.
Le nombre a (n) de briques nécessaires
pour atteindre le surplomb n est donné par la suite
A014537 de l'encyclopédie des suites de Sloane (http://www.research.att.com/~njas/sequences/A014537).
Un petit calcul montre que pour augmenter la longueur du surplomb
d'une brique, il faut multiplier le nombre de briques par environ
e2= 7,389...
Martin Gardner,
qui présenta cet empilement dans Scientific American en novembre
1964,
le désigne par le « paradoxe du surplomb infini
».
Considérer
l'empilement avec la série harmonique comme le meilleur possible
semblait admis.
Peut-être
ferez-vous mieux...

Villa Méditerranée près du MuCEM Marseille
CF aussi
http://www.pourlascience.fr/ewb_pages/a/article-surplombs-maximaux-18382.php