Un
triangle avec trois nombres aléatoires
?
Le
problème
On
tire 3 nombres réels au hasard, entre 0 et un maximum donné
(ici arbitrairement le maximum est fixé à 370) .
Quelle est la probabilité
pour que ces 3 nombres soient les longueurs d’un triangle non
aplati ?
Modélisation
Choisir
en cochant la case adéquate :
-simulation avec construction des triangles ou
-NON.
Choisir
le nombre d'expériences à réaliser*.
Si on trace les triangles, on peut moduler la
vitesse de tracé avec le curseur Vitesse.
Pour des raisons pratiques d'affichage, seules deux décimales
des longueurs sont affichées.
Cependant, elles sont toutes calculées dans le tirage et effectives
dans le tracé.
On peut visualiser
- la construction pas à pas des triangles OU bien v
- les points de coordonnées x , y et z correspondant aux longueurs
des côtés.
Il s'agit d'une coupe arbitraire réalisée avec une longueur
z à choisir pour comprendre le résulat final.
Cependant les résultats
sont simulés et calculés avec les différentes
valeurs aléatoires de z.
Les points sont verts quand le triangle
est constructible, rose foncé quand
ce n'est pas possible.
Notons
que lorsque z est nul, la surface verte devient un segment : la diagonale
du carré.
Lorsque z atteint la limite maximale, la surface verte devient triangulaire
: un demi-carré.
En répétant la simulation, on peut deviner ainsi la
forme du solide constitué des triplets (x, y, z) permettant
la construction d'un triangle.
500 000
points donnent une bonne représentation.
*ATTENTION à
bien appuyer la touche ENTREE pour valider les valeurs numériques
frappées,
si l'on choisit d'indiquer le nombre d'expériences ou le niveau
de coupe en Z au clavier.
CLIQUER

ANALYSE
Choisissons
comme unité de mesure la longueur maximale.
On obtient ainsi simultanément trois morceaux de longueurs
respectives x, y et z.
L a condition de constructibilité d'un triangle donné
par 3 longueurs prises entre 0 et 1 se traduit par les conditions
:
| x - y | < z < x + y pour (x,y,z) dans [ 0,1 ]3.
FINALEMENT
Pour chaque z trouvé,
0 < x < 1,
0 < y < 1,
x + y - z >
0,
si x > y, x - y - z < 0,
si x < y, y - x - z < 0,
donnent
l'ensemble les cas favorables
à chaque niveau du solide cherché.
C'est
la zone verte de la figure ci-dessous.
L'aire de cette surface en fonction de z est :
A(z) = 1 - z²/2 - 2 (1 - z)² / 2
soit
A(z) = 2 z - 3z²/2.
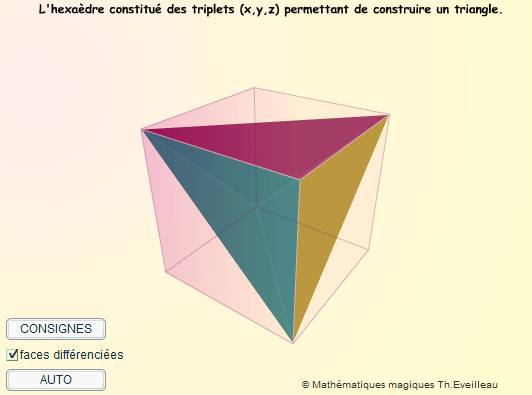
| Toutes
les surfaces empilées donnent un hexaèdre contenu
dans le cube unité.
Les points de coordonnées (x,y,z) doivent être
dans cet hexaèdre pour que le triangle de côtés
x, y et z soit constructible : cas
favorables.
Pour trouver le
volume de l'hexaèdre, nous allons intégrer la
surface A(z) par
rapport à z qui varie de 0 à 1.
V = 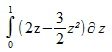 = =
 = 1 - 1/2
= 1 - 1/2
= 1/2.
Le cube
unité représente l'ensemble de tous les cas
possibles.
La probabilité se
traduit par le rapport des volumes : p = 1/2
soit p
= 50%.
La probabilité de construire un triangle dont les longueurs
des côtés ont été choisies au hasard
parmi les nombres compris entre 1 et L est de 50%.
|
|
L'hexaèdre à animer en mode AUTO, CLAVIER ou SOURIS
Cliquer
le bouton adéquat pour que l'hexaèdre aient des faces
coloriées différemment ou non.
CLIQUER
On
peut d'ailleurs vérifier que le volume de l'hexaèdre
est bien exactement la moitié de celui du cube unité
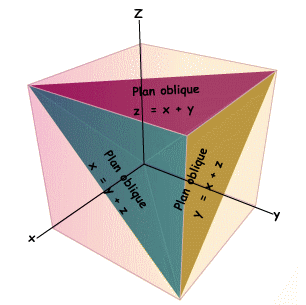
: il est obtenu en coupant le cube unité par les trois plans
obliques d'équations :
z = x + y ;
y = x + z ;
x = y + z.
Ainsi on enlève au cube unité trois pyramides dont chacune
a pour base un triangle rectangle isocèle de côté
1 (sur l'angle droit) et pour hauteur 1.
Chaque pyramide a pour volume (1²/2)/3 = 1/6.
Les trois pyramides ont un volume de 3(1/6) = 1/2 et enfin
l'hexaèdre a un volume de 1 - 1/2 = 1/2.
La boucle est bouclée. Hum... disons le triangle est clos.