Problème

Dans un carré ABCD, on note (m) la médiatrice de [AB] et (n) celle de [AD].
Soit T un triangle APQ, rectangle en A, tel que P soit sur (m) et Q sur (n).
Montrer que APQ est isocèle et qu’il existe deux positions du triangle T pour lesquelles (PQ) passe par C.
On note P1, Q1 et P2, Q2 les points correspondants.
Montrer que les triangles ABP1, ABP2, ADQ1, ADQ2, CP1Q2, CP2Q1 sont de même nature.
Mettre en évidence un septième triangle de même nature.

Suite... si on construit deux triangles ABP et ADQ équilatéraux
en haut et dans le carré ABCD (CF figure en bas de page) alors les points P, Q et C sont alignés.

Figure animée

Sur la figure suivante, déplacer le point P sur la médiatrice.
On peut aussi modifier le carré avec le point (éventuellement le point B. Observer, analyser...

SOLUTION et Démonstration

La figure suivante met en évidence les six triangles équilatéraux ABP1, ABP2, ADQ1, ADQ2, CP1Q2, CP2Q1
et le septième CW1W2.

Les sept triangles équilatéraux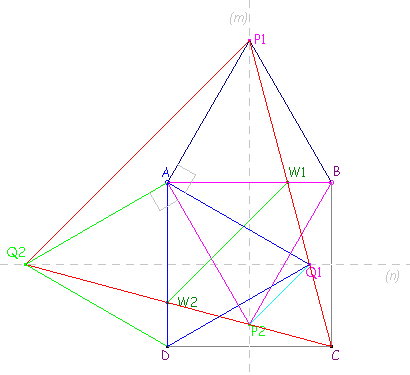

Analyse préalable de la figure Dans la rotation de centre A et d'angle -90° : - la droite (m) a pour image (n) - la droite (AP1) a pour image (AQ1) P1 qui est l'intersection de (m) et (AP1)      a donc pour image Q1 qui est l'intersection de (n) et (AQ1). On en déduit que AP1 = AQ1 et que le triangle rectangle P1AQ1 est isocèle. Les quatre triangles ABP1, ABP2, ADQ1, ADQ2 sont isocèles pour raison de symétrie par rapport aux médiatrices (m) ou (n). Les triangles ABP1 et ADQ1 se déduisent l'un de l'autre par une rotation de centre A et d'angle 90°. Ils sont donc superposables. Si l'un est équilatéral l'autre le sera. Par une rotation de la figure d'un quart de tour, nous obtiendrons les deux triangles ADQ2 et ABP2 à partir de ABP1, ABP2. Ils seront donc tous superposables et de même nature (remarque 0). Pour les trois derniers triangles isocèles CP1Q2, CP2Q1, CW1W2 (symétrie par rapport à (AC) ), il suffira de montrer que l'un de leurs angles mesure 60°.

Montrons que le triangle ABP est équilatéral

Comme le triangle ABP est isocèle avec AP = PB, il suffit de prouver que AB = AP ou AB = BP.

Démonstration

 

Le triangle ABP est rectangle isocèle donc l'angle APB mesure 45°. L'angle ABC mesure 90°. L'angle APC mesure 45° (alignement de P, Q et C). On sait donc donc que le point P est sur l'arc capable d'où l'on voit [AC] sous un angle de 45°. Cet arc est porté par le cercle de centre B et de rayon AB = BC. L'angle en B de 90° étant angle au centre et l'angle en B, un angle inscrit. Dans ce cercle, on a AB = BP. Ceci prouve que le triangle isocèle en P, ABP est équilatéral. Grâce à la remarque 0 .nous déduisons que les quatre triangles ABP1, ABP2, ADQ1, ADQ2 sont équilatéraux.

Remarque Une autre démonstration consiste à montrer que les triangles PBQ et AQC sont superposables (un angle égal compris entre deux côtés égaux). On en déduit alors que PQ =AC et donc que PQ = AD . Dans le triangle erctangle isocèle APQ on a PQ = AP, on en déduit que AP = AD,soit AP = AB et donc ABP équilatéral.

Montrons maintenant que l'angle W1CW2, mesure 60°

Il suffit de montrer que W1CA mesure 30° ou que W1CB mesure 15° puisque ACB mesure 45°. Le triangle PBC est isocèle car PB = BC. Ses deux angles à la base ont même mesure : ( 180° - (90° + 60°) ) / 2 = 15° Donc l'angle BCP mesure 15°, puis ACW1 mesure 45°- 15° = 30° et enfin par symétrie par rapport à (AC) W1CW2, mesure 60°.

Ainsi les trois derniers triangles isocèles CP1Q2, CP2Q1 et CW1W2, qui ont un angle de 60° sont équilatéraux.

 

Suite... Si les triangles ABP et ADQ sont équilatéraux alors les points P, Q et C sont alignés

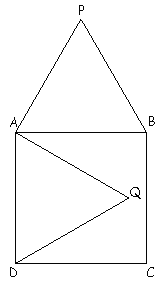
Figure
Les triangles ABP et ADQ sont équilatéraux.
Montrer que les trois points P, Q et C sont alignés.


Démonstration

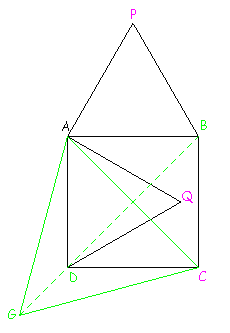Traçons le triangle équilatéral AGC. (BG) est un axe de symétrie de ce triangle. C'est la médiatrice de [AC] et donc c'est aussi (BD). G, D et B sont alignés. . Dans la rotation de centre A et d'angle 60°, l'image de G est C ; l'image de de D est Q ; l'image de B est P. La droite formée par les points G, D et B a donc pour image une droite passant par C, Q et P. Ceci prouve que les points C, Q et P sont alignés.