Le
trisecteur et les trisectrices...
|
|
 L'instrument
et son
mode d'emploi L'instrument
et son
mode d'emploi
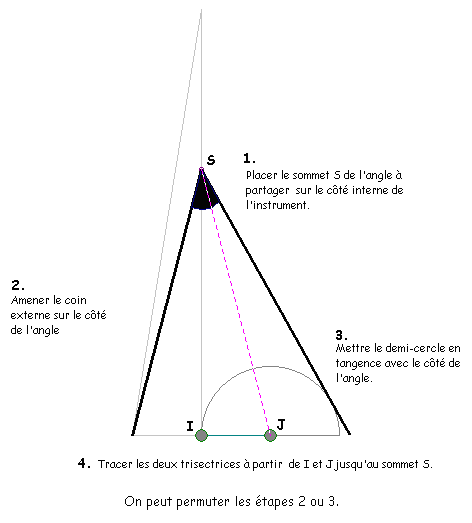
Le
trisecteur permet de partager un angle en trois angles de même
mesure.
Il se compose d'un triangle rectangle accolé à un demi-cercle,
dont le rayon a même mesure que le petit côté de
l'angle droit du triangle.

 Manipulons Manipulons
Fixer d'abord
la mesure de l'angle, en déplaçant le point A
appartenant au côté de l'angle.
L'angle est reporté sur l'instrument.
Positionner le point S jusqu'à ce
que le côté droit de l'angle rose soit tangent au cercle.
Alors la trisection apparaîtra aussitôt.
La précision est d'environ 1 pixel. Il convient de
déplacer doucement les points.
Chaque point peut être déplacé à la SOURIS
ou au CLAVIER.
Quatre flèches
de direction pour le point A et seulement
Haut et bas pour le point S.
Autre
animation interactive
Cette fois on déplace le trisecteur en le draguant avec la
souris en la plaçant au coin du bas à gauche.
On le fait tourner dans un sens ou l'autre avec la flèche
;
On modifie l'angle de sommet O, en déplaçant l'un
des trois points O, C ou D.
Quand le trisecteur est correctement placé, les demi-droites
vertes délimitent trois angles de même mesure.
CLIQUER
Rappelons
que la méthode est rigoureuse et parfaite comme l'indique la
démonstration qui suit.
Cependant la manipulation ne peut que donner un résultat approché
au degré près, en voici un exemple ci-dessous.
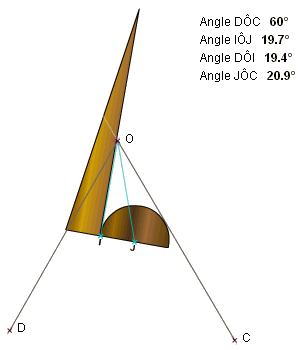

 Explications Explications
| 
|
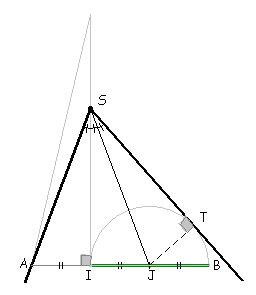
Nous avons
l'égalité :
AI = IJ = JB et l'angle AIS est droit.
 Dans
le triangle ASJ (SI) est hauteur et médiane, le triangle
est donc isocèle et (SI) est aussi bissectrice de l'angle
ASJ. Dans
le triangle ASJ (SI) est hauteur et médiane, le triangle
est donc isocèle et (SI) est aussi bissectrice de l'angle
ASJ.
 Les
deux segments [IJ] et [JT] sont perpendiculaires
aux côtés [SI) et [ST) de l'angle IST. Les
deux segments [IJ] et [JT] sont perpendiculaires
aux côtés [SI) et [ST) de l'angle IST.
Ils sont de même mesure, la droite (SJ) est donc bissectrice
de l'angle IST.
On a bien égalité
des mesures des 3 angles déterminés par (SI) et
(SJ). |
Bien sûr,
on peut percevoir les limites selon la taille du trisecteur.

|