 Truc
: pour
calculer de tête le carré d'un nombre se terminant
par 5.
Truc
: pour
calculer de tête le carré d'un nombre se terminant
par 5.
On prend le nombre de dizaines multiplié par son successeur.
Cela donne le nombre de centaines du résultat.
On écrit alors 25 à droite du nombre de centaines
pour obtenir le résultat.
Exemples
:
35 est composé de 3 dizaines et 5 unités, son
carré s'obtient :
nombre de centaines : 3*4=12, le
carré est 1225
65 est composé de 6 dizaines et 5 unités, son
carré s'obtient :
nombre de centaines : 6*7=42, le
carré est 4225
105 est composé de 10 dizaines et 5 unités,
son carré s'obtient :
nombre de centaines : 10*11=110,
le carré est 11025
Justification
Soit (10d + 5) le nombre qui s'écrit avec d comme nombre
de dizaines et 5 comme chiffre des unités.
Avec 45 par exemple, nous avons d = 4 et avec 235
nous avons d = 23.
Alors
(10d + 5)² = (10d)² + 2x10dx5 + 5²
(10d + 5)² = 100d² + 100d + 25
(10d + 5)² = 100d(d+1) + 25
Le résultat a pour nombre de centaines le produit d(d+1).
On écrit 25 à droite du produit d(d+1) et on obtient
donc le résultat final.
Application avec un
nombre quelconque ne se terminant pas par 5 :
il suffit de se ramener avec une addition ou une soustraction à
un nombre se terminant par 5 voire par 0.
Il faut alors utiliser les identités remarquables et être
bon en calcul mental.
Exemples
:
83² = (80 + 3)² = 80² + 2x3x80 + 3² = 6400 + 480 + 9 = 6889.
Ici il est inutile d'utiliser 85²
Mais on pourrait faire 83² = (85 - 2)²= 85² - 2x2x85 + 4
= 6889
87² =
(85 + 2)² = 85² + 2x2x85 + 2² = 7225 + 340 + 4 = 7569
et
88² = (85 + 3)² = 85² + 2x3x85 + 3² = 7225 + 510 + 9 = 7744
Ce dernier exemple peut aussi être traité ainsi : 88²
= (90 - 2)² = 8100 -2x2x90 + 2² = 7744.
En général on préfère utiliser une addition.
 Autre
truc :
pour
multiplier deux nombres de deux chiffres dont les dizaines sont
égales et dont la somme des chiffres des unités est
10.
Autre
truc :
pour
multiplier deux nombres de deux chiffres dont les dizaines sont
égales et dont la somme des chiffres des unités est
10.
Exemple
:
47 x 43 = 2021 (car 4x(4+1) = 20 et 7x3=21)
36 x 34 = 1224 (car 3x(3+1) = 12 et 6x4=24)
51 x 59 = 3009 (car 5x(5+1) = 30 et 1x9=09)
Justification
Soit d le nombre de dizaines et u le chiffre des unités du
premier nombre.
Le produit est donc
(10 d + u) (10d + (10 - u))) = 100d2 + 10du + 100d +
10u -10du -u2
(10 d + u) (10d + (10 - u))) = 100d2 + 100d + 10u - u2
(10 d + u) (10d + (10 - u))) = 100d(d+1) + u(10-u)
Exemple avec un nombre de 3 chiffres
:
126 x 124 = 15624 (car 12x(12+1) = 156 et
6x4=24)
 Exemples
de nombres quelconques
:
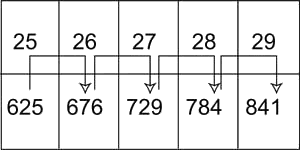
Exemples
de nombres quelconques
:
|
Par exemple
:
262
= 625 + 25 + 26
Donc
262
= 676 |
 Une
autre exploitation
Une
autre exploitation
connaissant le carré de 40, retrouver le carré de
39 par soustraction :

|
Par exemple
:
392
= 1600 - 40 - 39
Donc
392
= 1521 |
Principe
: n2 = (n+1)2 - (n+1) - n .