---

 

SOLUTION

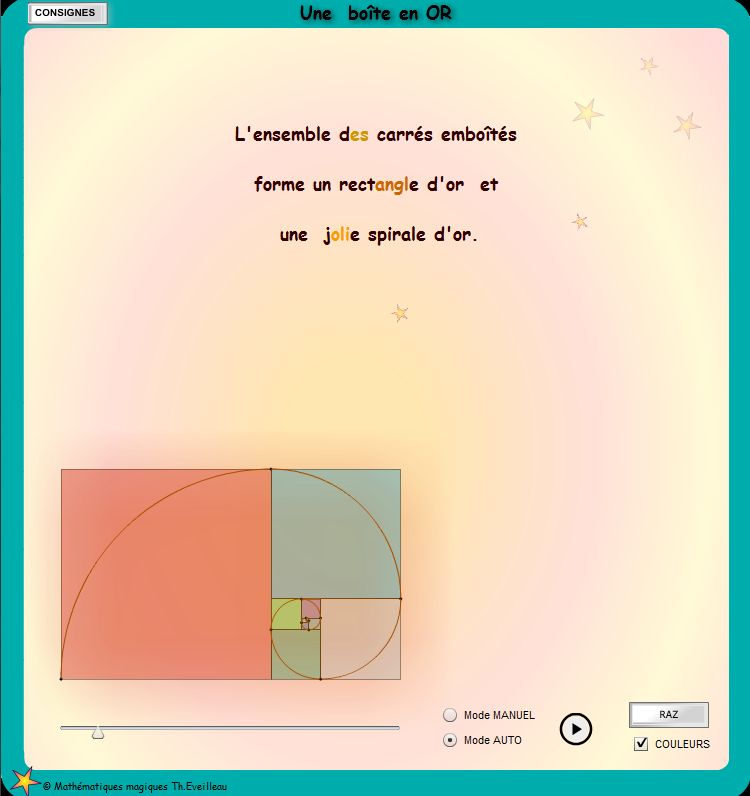
.Des carrés dans un rectangle d'or

 

 

.EXPLICATIONS

Choisissons un rectangle de longueur r unités et de largeur 1 unité.
Son aire est r = 1*r.

Le plus grand carré est de côté 1 ;
le carré suivant est de côté r - 1 et d'aire (r - 1)² ;
le suivant est de côté 1 - (r - 1) = 2 - r et d'aire (2 - r)² ;
ensuite les côtés sont : r - 1 - (2 - r) = 2 r - 3 ;
puis 5 - 3r ;
puis 5r - 8 ;
puis 13 - 8r etc.

Nous reconnaissons des coefficients qui sont les termes de la suite de Fibonacci.

En remontant cette suite de la fin vers le début,
c'est-à-dire du plus petit carré vers le plus grand, nous obtenons une suite de Fibonacci : chaque terme étant la somme des deux précédents.

OR les termes de la suite de Fibonacci vérifient la propriété suivante :
la somme des carrés n premiers nombres issus de la suite de Fibonacci, est égale au produit du dernier terme de la suite et du suivant.

F0² + F1² + F2² + ... + Fn² = Fn * Fn+1

EEn partant du carré de côté infiniment petit, le nombre de termes est infini,
ET Fn-1 = r-1 ; Fn = 1 ; Fn+1 = r

La somme des aires de tous les carrés est :
... + (13 -8r) ² + (5 -3r) ² + (2r -3) ² +(2 -r) ² + (r-1) ² + 1 ² = 1 * (r - 1+1) = 1 * r

SOIT
... + (13 -8r)² + (5r -8)² + (5 - 3r)² + (2r - 3)² + (2 -r)² + (r - 1)² + 1 ² = r

On vérifie ainsi par le calcul que La somme des aires de tous les petits carrés ainsi construits
donne bien logiquement l'aire du grand rectangle.


Partons d'un rectange d'or dont les côtés sont 1 et le nombre d'or : Φ .
Ce rectangle d'or contenant des carrés dont les côtés sont obtenus en divisant le côté du carré précédent par Φ.

Vérification avec la relation sur le nombre d'or : Φ² - Φ - 1 = 0.

La suite des carrés a pour côtés :
1 ;
Φ-1 = 1/Φ ;
2 - Φ = 1/Φ²;
2Φ - 3 = 1/Φ³ etc.
Nous obtenons une suite géométrique de raison 1/Φ.

La somme des aires de tous les carrés est la somme infinie des termes d'une géométrique de raison 1/Φ².
Cette somme est 1/(1-1/Φ ²) = Φ² /( Φ² - 1) = (Φ + 1) / Φ = Φ² /Φ = Φ.

 

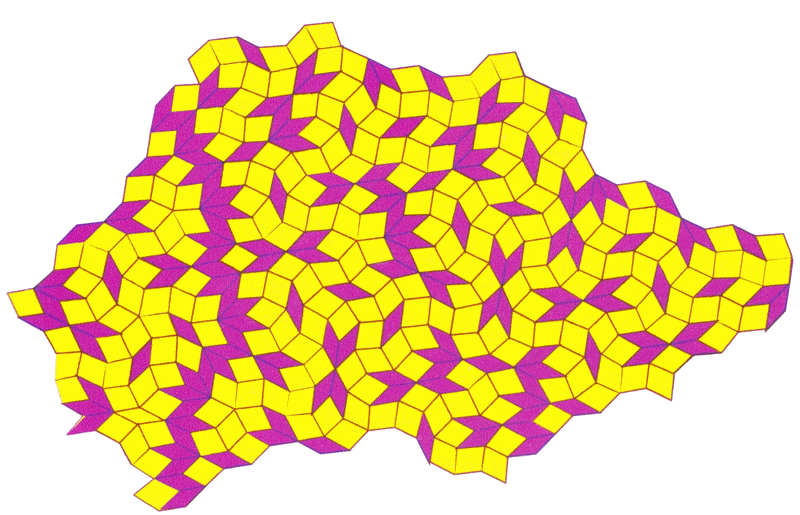
Dans un pavage de Penrose, les angles des quadrilatères sont liés au nombre d'or.
Tant que l'on continuera la construction du pavage, on ne retrouvera jamais de répétition parfaite.