Une
droite est dite coupée en EXTREME et MOYENNE RAISON
Lorsque la droite entière est à son plus grand segment
ce que
le plus grand segment est au plus petit
EUCLIDE
les éléments
|
|
Des vidéos
en liens externes :
Nombre
d'or, Section dorée, Divine proportion et autres apellations
mystiques... sont des dénominations qui désignent un rapport
arithmétique : le nombre d'or. Ce dernier n'est ni une mesure,
ni une dimension, c'est un rapport entre deux grandeurs homogènes.
Jean-Paul Delahaye affirme (pour
la Science Août 1999) que le chemin des mathématiques
à la numérologie est dangereux parce riche en interprétations...
En effet des milliers de pages ont été écrites
sur le nombre d'or, baptisé Φ. Il serait connu depuis la nuit des
temps. On le retrouve chez les peintres du début du siècle,
dans les cathédrales gothiques, sur les façades des temples
grecs et même au cœur de la Grande Pyramide. On dit qu'il
aurait été transmis de bouche de pyhtagoricien à
oreille d'initié, comme un secret universel et immuable (il n'était
pas considéré comme un nombre puisque seuls les entiers
sont des nombres chez les grecs). De nombreux tableaux seraient conçus
selon les règles de la "divine proportion" (expression datant
de 1509 avec Léonard de Vinci).
Parmi les artistes de la Renaissance, Dürer est un de ceux qui
connaissait les mathématiques. Il fit évoluer les proportions
de "ses nus d'Adam et Eve", entre 1504 et 1507 après
avoir été initié à la "secretissima
scienta" par un maître dont il ne voulut pas révéler
le nom mais qui fut sans doute le frère franciscain Luca Pacioli
qui publia en 1494 la grande encyclopédie du XVe siècle.
| 
|
Certains peintres comme Salvador Dali (Sacrement
de la dernière cène),
Seurat (le Cirque) ou Mondrian (Composition) l'ont d'ailleurs
utilisé par jeu.
Le nombre d'or véritable petit nirvana arithmétique
a été une voie privilégiée de communication
avec l'au-delà... |
 |
| 
|
Cirque de Georges
Seurat (Musée d’Orsay 1890-1891).
Les lignes horizontales tracées dans le tableau ont des
grandeurs proportionnelles à Φ. Il en serait
de même pour la loge délimitée par des lignes
de couleur rouge vif formant un rectangle d’or. L’utilisation
du nombre d’or dans ce tableau est opposée aux lignes
courbes du personnage central du tableau ainsi qu’aux autres
acrobates. Le nombre d’or met donc en valeurs les lignes
géométriques des bancs. |
Rythmes
musicaux
Aux mesures traditionnelles à deux ou à trois temps,
2/1 ou 3/2 s’ajoutent des éléments rythmiques
de type 5/3 ou 8/5 (jazz ou musique orientale…)
Nous retrouvons la suite 1-1 2-3-5-8…
de Fibonacci.
Structures musicales
De nombreux exemples montrent que la proportion des diverses parties
d’une œuvre est souvent réglée dans le rapport
8/5, voisin de Φ
. C’est le cas chez Haydn,
Mozart ou Beethoven.
Rythmes poétiques
Dans la métrique des vers, soit par la césure, soit
par l ’alternance de vers ayant un nombre de pieds différents,
nous retrouvons les nombres de la suite traditionnelle de Fibonacci.
Que j ’aime voir, chère
indolente,
De ton corps si beau, (8/5)
Beaudelaire
Les cors, les cors, les cors mélancoliques !
Mélancoliques ! (10/6=5/3)
Jules Laforgues
Dans la nuit éternelle | emportés sans retour ( ou 1/1)
Ne pourrons nous jamais sur l ’océan des âges.
Jeter l ’ancre un seul jour (12/6=2/1)�
Lamartine
Avant de me dire ta peine�O poète !
En es-tu guéri ?
La Muse (12/8 = 3/2)
A de Musset
En réalité avec quelques
approximations il est très facile d'approcher le nombre d'or.
Marguerite Neveux a démontré qu'en réalité
les artistes divisaient leurs toiles en huitièmes, ce qui est
très facile, puis en 4/8 et en 5/8 qui est très proche
du nombre d'or à 7 millièmes près. Cette petite
différence a suffi à créer bien des rêves
dorés et à déchaîner des passions qui retombent
actuellement (les fractales sont aujourd'hui plus motivantes).
Notons que le format le plus utilisé est le fameux 21/29.7...
(A4, A3,...) seul format qui
plié en deux garde la même forme : rapport  . .
Tout de même le nombre d'or a des propriétés mathématiques
bien réelles et on le retrouve dès qu'on a une symétrie
d'ordre 5. Nous l'avons déjà rencontré avec les
lapins de
Fibonacci, dans les morceaux
disparus...
Nous allons en découvrir quelques unes de ses propriétés
mathématiques.
Si vous ne l'avez pas effectué, n'hésitez pas à
faire le petit test.
 Le
nombre d'or, définition Le
nombre d'or, définition
Ce
nombre est la valeur d'un rapport de deux grandeurs homogènes.
Il est déterminé par une proportion :
Il
y a de la petite partie à la grande, le même rapport
que la grande au tout
(Vitruve,
architecte romain 1er siècle avant notre ère).
Ainsi si a et b sont les deux grandeurs alors nous aurons :
a/b
= (a + b) / a.
a/b
= 1 + b/a
pour simplifier,
prenons comme variable x
= a/b.
alors nous obtenons :
x =
1 + 1/x
x - 1 - 1/x = 0
comme x non
nul, nous obtenons l'équation suivante que nous noterons
(E)
:
x2
- x - 1 = 0
qui admet
comme racine positive :
x =
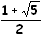
que nous notons
Φ
et vaut à peu près 1,618...
C'est cette valeur
qui est appelée le nombre d'or (dit Φ
(phi) en hommage au sculpteur grec Phidias qui
s'en servit dans les proportions du Parthénon à Athènes.
En espagne, deux
tableaux de Antonio de Garcia de Pablo, muchas gracias ;):
Pour voir les images suivantes en plus grand les cliquer
A
ce stade, je vous soumets un petit problème que m'a proposé
Dominique Payeur :
Je dispose d'un capital.
Celui -ci augmente deux années de suite du même pourcentage
puis diminue la troisième année de ce même pourcentage.
Curieusement je retrouve alors le capital de départ.
Par combien est multiplié le capital la première
année ?
Quel est le pourcentage du placement de mon capital les deux premières
années ?
Et... quel est le rapport avec le thème de cette page ?
La solution ICI
Nous pouvons d'ores
et déjà noter quelques résultats :
Φ2
- Φ
- 1 = 0
Φ
=
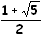
Pour
obtenir le carré , on ajoute l'unité :
Φ2
= Φ
+ 1
Pour
obtenir l'inverse, on soustrait l'unité :
1/Φ
= Φ
-
1
|
On pourrait
aussi sans équation du second degré montrer que
1/Φ
= Φ
-
1.
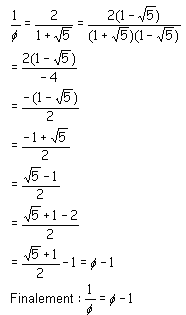
Des équations
précédentes, nous pouvons déduire : x2
= x + 1 et x = 1 + 1/x d'où
 et
on
a aussi : et
on
a aussi :

Le
nombre d’or peut s’écrire à l’aide
d’une infinité de radicaux emboîtés
CLIQUER

Les FRACTIONS
CLIQUER
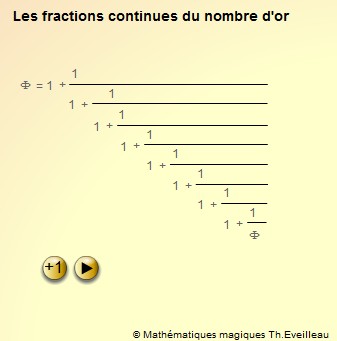
A
l'aide des deux formules précédentes on peut approcher
de très près la valeur du nombe d'or.
Il suffit de partir d'une valeur arbitraire.
On obtient alors les valeurs obtenues à l'aide de chacune
des deux formules.
Entrer ci-dessous la valeur de départ dans
le bouton adéquat.
Si la valeur est entrée au clavier SURTOUT ne PAS OUBLIER
de frapper la touche ENTREE ensuite.
Pour
effectuer les calculs avec chaque formule,
appuyer sur la flèche droite
en bas à droite de l'animation (le n°
de l'itération augmente à chaque appui).
A chaque fois, Φ0
prend la dernière valeur obtenue comme approximation de Φ
et le calcul est réeffectué avec cette valeur de Φ0.
Répéter le procédé autant que l'on veut.
Le résultat est de plus en plus précis :
comparer avec la vraie valeur affichée en bas de l'animation.
CLIQUER

J'ai limité le nombre d'itérations à 50 pour
des raisons liées au logiciel : on voit que les valeurs stagnent
à partir d'un certain moment : on atteint les limites de
la précision du calcul de l'ordinateur.
Nous pouvons noter que la convergence vers une 'bonne' valeur est
très rapide.
Partons
de deux nombres quelconques :
102 et 75 par exemple.
Construisons alors les autres termes en appliquant la règle
d'une suite de Fibonacci :
chaque nouveau terme étant obtenu en ajoutant les deux précédents.
75, 102, 177, 279, 456, 739...
Effectuons le quotient de deux nombres consécutifs. Le résultat
tend rapidement vers le nombre d'or :
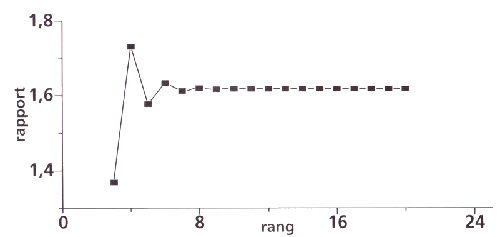
Voir
un petit tour magique
basé sur le nombre d'or ICI.
A l'intérieur du système formé des mesures
qui sont des termes d'une suite géométrique de raison
Φ
,
les
multiplications, divisions, élévations aux puissances
et extractions de racines peuvent être remplacées par
des additions et soustractions, ce qui rend le calcul abordable
à des personnes ne sachant que compter comme c'était
le cas dans les systèmes anciens de numération (pensons
aux chiffres romains...).

 Le
rectangle d'or Le
rectangle d'or
Un
rectangle
d'or est un rectangle dont le rapport longueur sur largeur est égal
au nombre Φ.
On part
d'un côté de longueur 1/2 pour construire un triangle
rectangle dont les côtés de l'angle droit mesurent
1 et 1/2.
En utilisant le théorème de Pythagore, l'hypoténuse
mesure  . .
Il suffit de terminer le rectangle d'or dont les côtés
mesurent 1 et
Φ
=
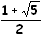 . .
Ce rectangle est harmonieux, son équilibre flatte l'oeil
et statistiquement il a la préférence lorsqu'on le
compare à d'autres rectangles de formes diverses.
Voir
d'autres formats de rectangles : A4 B5... ICI.
CLIQUER
Savez-vous
que la plupart de vos cartes quotidiennes sont formatées
avec le nombre d'or ?
Une façon de le vérifier est de les disposer comme
ci-dessous.
La diagonale de la première carte aboutit exactement sur
un sommet de la deuxième.

ANIMATION expliquant
cette propriété
cliquer les flèches pour avancer ou reculer pas à
pas.
CLIQUER

 La
spirale du rectangle d'or La
spirale du rectangle d'or
Cette
spirale est une 'fausse' spirale parce qu'elle est constituée
d'arcs de cercles au lieu d'avoir une variation continue du rayon.
Cependant les raccordements des arcs sont parfaits car la condition
de tangence est respectée. Les centres des arcs sont à
chaque fois situés sur la même droite perpendiculaire
à cette tangente. Cette
courbe est connue sous le nom de 'spirale logarithmique'. Elle s'enfonce
sans fin et tend rapidement vers un point Z autour duquel elle s'enroule
de plus en plus près. Ce point est appelé le centre
de la spirale. Appelée spirale de Bernoulli, elle a de nombreuses
propriétés. L'une d'elles est que le segment de droite
qui joint le centre Z à un point de la courbe croît
en progression géométrique. La longueur du rayon vecteur
est multipliée par le nombre d'or chaque fois que sa direction
tourne d'un quart de tour. Par contre l'angle que fait ce segment
avec une direction de départ quelconque, croît en progression
arithmétique.
CLIQUER
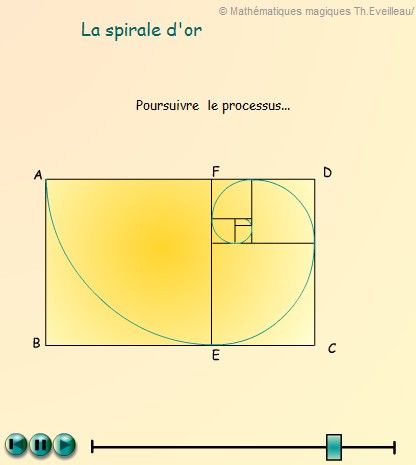
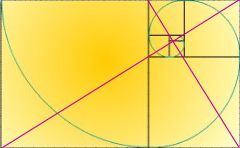
Si
nous traçons une diagonale entre le coin supérieur
droit et le coin inférieur gauche, puis entre le coin supérieur
gauche et le coin inférieur droit du rectangle d'or plus
petit, le point d'intersection est le point de convergence de tous
les rectangles d'or plus petits. De plus, le rapport des longueurs
de ces deux diagonales est égal au nombre d'or. On appelle
quelquefois l'il de Dieu le point de convergence de tous les rectangles
d'or.
|
 Pourquoi
une suite de rectangles d'or ? Pourquoi
une suite de rectangles d'or ?
Le
premier rectangle a des côtés de longueur
1
et
Φ
dont le rapport est Φ.
Le deuxième rectangle a des côtés de
longueur Φ
-
1
et
1
soit
1/Φ
et
1
dont
le rapport est Φ.
Le troisième rectangle a des côtés de
longueur 1
- 1/Φ
=
1/Φ2,
soit
1/Φ2
et 1/Φ
dont le rapport est Φ.
Le quatrième rectangle a des côtés de
longueur 1/Φ
-
1/Φ2
=
1/Φ3
et
1/Φ2,
soit
1/Φ3
et 1/Φ2
dont le rapport est Φ.
...
Le nième rectangle a des côtés
de longueur
1/Φn-3
-
1/Φn-2
=
(Φ
-
1)/Φn-2
= (1/Φ)/
Φn-2
= 1/Φn-1
et 1/Φn-2,
soit
1/Φn-1
et 1/Φn-2
dont le rapport est Φ.
Nous
avons donc bien une suite de rectangles d'or.
|

SUITE



(1)ROBERT VINCENT
Géométrie du nombre d'or éditions chalagam
L'art des batisseurs romans association des amis de l'abbaye
de Boscodon
CLAUDE JACQUES WILLARD Le nombre d'or éditions Magnard
JEAN-PAUL DELAHAYE Pour la Science Août 1999
ORTOLI WITKOWSKI La baignoire d'Archimède Sciences
Le nombre d'or Que-sais je ?
LUCAS PACIOLI La divine proportion éditions Navarin
MATILA GHYKA Le nombre d'or éditions Gallimard
WARUSFEL Les nombres et leurs mystères éditions
du Seuil
D. NEROMAN Le nombre d'or clé du monde vivant Dervy-livres,
6 rue de Savoie, Paris V
 Solution
du problème du capital Solution
du problème du capital
Choissons C
la variable désignant le montant du capital et T %
le taux (positif) du placement.
Posons t = T/100
. A la fin de la première année
le capital a donc augmenté de T %.
Il est devenu :
C + t C soit (1 + t ) C
. A la fin de la deuxième année
ce capital (1 + t ) C a encore augmenté de T
%.
Il a été multiplié une nouvelle fois par (1+
t ) et est devenu :
(1+ t) (1+ t) C soit (1 + t)2 C
. A la fin de la troisième année
le nouveau capital (1 + t)2 C a diminué
de T %.
Il a été multiplié par (1 - t) et est devenu
:
(1 + t)2 (1 - t) C
Et nous obtenons le capital initial d'où :
(1 + t)2 (1 - t) C = C
Cela implique que : (1 + t)2 (1 - t) = 1
Donc (1 + t) (1 - t) (1 + t) = 1
Soit (1 - t2) (1 + t) = 1
Ou 1 - t2 + t - t3 = 1
Finalement nous obtenons :
- t2 + t - t3 = 0
ou - t + 1 - t² = 0
ou t² + t - 1 = 0
Cette équation a pour racine racine positive (la
seule qui nous concerne) :
t = (- 1 + 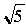 )
/2 soit
t
= )
/2 soit
t
= 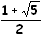 - 1
- 1
Et
nous avons t = Φ
- 1 ;
t vaut environ
0,618. Le taux est donc d'environ 61,8%
Ainsi le capital
initial est multiplié chacune des deux premières années
par (1+t).
Ce capital est donc multiplié par
le nombre d'or Φ.
Cela correspond à un taux d'environ 61,8%.
Remarque :
Comme
t
= Φ -
1
nous avons 1 + t = Φ et 1 - t = 2
- Φ.
A la fin des deux premières années le capital est
multiplié par (1 + t)2
soit par Φ2
et
à la fin de la troisième année le capital est
multiplié par (1 - t) = 2
- Φ.
Ainsi au bout des trois années, le capital a été
multiplié par
Φ2
(2 - Φ)
= (Φ + 1)
(2 - Φ)
car Φ2
= Φ + 1
=
2Φ + 2 -Φ2
- Φ
=
Φ
+ 2 - Φ 2
=
(Φ
+ 1) + 1 - Φ 2
=
Φ
2 + 1 - Φ
2
=
1
Voilà pourquoi au bout de trois ans on retrouve le capital
initial : il a été multiplié par 1.

|




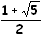



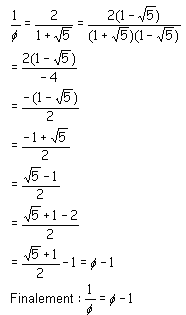
 et
on
a aussi :
et
on
a aussi : 









