Le nombre d'or

Un petit test Le nombre d'or, définition Le rectangle d'or, sa spirale Le triangle d'or, sa spirale, des démonstrations Un petit tour expliqué pour devenir un génie du calcul... Le pentagone des Compagnons 3 constructions du pentagone régulier Quine et nombre d'or Dans la nature Autres formats 34 spirales tournent dans le sens des aiguilles d'une montre et 21 spirales tournent dans l'autre sens.

1       1       2       3       5       8       13       21       34       55       89       144...

Le nombre d'or dans la nature

Feuilles et pétales
Coupons une pomme en deux dans le sens de son équateur, on y découvre les pépins disposés en une belle étoile à 5 branches. C'est aussi valable pour une poire. Le silène rose qui semble avoir 10 pétales, n'a en réalité que 5 pétales subdivisés en deux. Les boutons d'or ont 5 pétales, les marguerites ont généralement 34, 55 ou 89 pétales. Ces nombres font partie de la suite de Fibonacci liée au nombre d'or. La suite de Fibonacci intervient dans la nature.
Avec E.P Northrop dans Fantaisies et paradoxes mathématiques examinons la disposition des feuilles, bourgeons ou branches sur la tige d'une plante.
Prenons comme point de repère une feuille voisine de la base d'une tige qui porte des feuilles isolées. Numérotons cette feuille 0 et comptons les feuilles vers le sommet jusqu'à ce que nous arrivions à une feuille qui se trouve juste au-dessus de celle dont nous sommes partis. Le nombre de feuilles rencontrées est en général un terme de la suite de Fibonacci. De même en progressant vers le sommet, comptons le nombre de tours que nous faisons. Ce nombre est aussi, en général un terme de la suite de Fibonacci. Si le nombre de tours est m et si le nombre de feuilles est n, appelons cette disposition "spirale m/n". 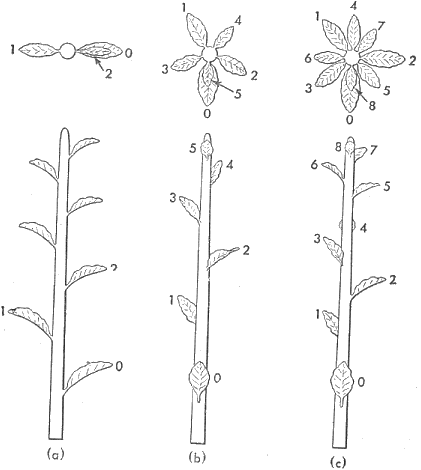Par exemple, la figure a) montre une spirale 1/2, vue latérale et par le bout. La longueur de la tige est exagérée de manière à montrer plus clairement les positions des feuilles. La disposition b) correspond à une spirale 2/5 ou 3/5 suivant les aiguilles d'une montre ou en sens inverse... On conviendra de choisir le plus long chemin et la disposition c) est une spirale de 5/8. On peut observer des dispositions semblables sur de très nombreuses variétés d'organes végétaux, pommes de pin, pétales de fleurs, feuilles de laitue, tuniques d'oignon... Les rapports mentionnés sont les rapports des termes successifs de la suite de Fibonacci.
La fleur normale de 12 à 15 cm de diamètre possède en général 34 spirales tournant dans un sens et 55 dans l'autre. Des fleurs plus petites peuvent présenter les combinaisons 21/34 ou 13/21 et des fleurs exceptionnellement développées peuvent aller jusqu'à 89/144.

Fruits d'Eucalyptus provenant de Galice en Espagne.
On trouve des pentagones réguliers, mais aussi des carrés er des triangles équilatéraux.

Lien avec l'ensoleillement
Cela vient de ce que l'ensoleillement doit être maximum pour toutes les feuilles et on démontre que l'angle de deux feuilles consécutives doit être voisin d'un certain k ^ème de tour ; les fractions de Fibonacci sont les fractions les plus voisines de k.

Toute feuille, tout pétale se présente d'abord sous la forme d'un petit bourgeon. Les bourgeons apparaissent l'un après l'autre sur la tige. Chacun essaie de s'éloigner le plus possible du précédent pour avoir le maximum d'espace et de lumière. Il se trouve qu'un angle en rapport avec le nombre d'or est particulièremenbt bien adapté : 360° divisé par F soit environ 222,5° dans un sens ou 137,5° dans le sens inverse. 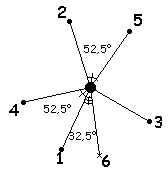C'est justement cet angle que l'on trouve dans les plantes. Ainsi si chaque bourgeon est ainsi tourné de 137,5° par rapport au précédent le sixième bourgeon n'est en décalage que de 32,5° par rapport au premier. Il se retrouve donc légèrement dans l'ombre du premier et a donc un peu moins accès au soleil et à la lumière que les autres bourgeons et c'est ce qui fait qu'il a très peu de chances de se développer et c'est peut-être une raison pour laquelle tant de plantes ne vont pas au-delà de cinq.

Les graines dans une fleur de tournesol 

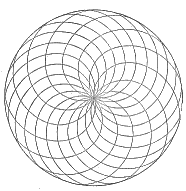
Disposition schématique des graines dans une fleur de tournesol ou de marguerite.

On rencontre fréquemment la spirale logarithmique dans la disposition des graines dans les fleurs, dans les coquilles d'escargot et autres. Dans un ananas ou une pomme de pin les écailles s'organisent en deux ensembles de spirales. L'un qui tourne dans le sens des aiguilles d'une montre, l'autre dans le sens inverse. Dans la fleur de tournesol, les graines sont aussi réparties en spirales qui rayonnent à partir du centre vers le bord. L'étude détaillée de ces spirales a conduit aux conclusions suivantes : les spirales sont logarithmiques le nombre des spirales dans le sens des aiguilles d'une montre et celui en sens inverse sont les termes successifs de la suite de Fibonacci. Sur l'exemple ci-contre nous avons 13 spirales tournant dans le sens des aiguilles d'une montre et 21 spirales tournant dans l'autre sens. cliquer ici pour voir les spirales d'une fleur de marguerite Les spirales logarithmiques sont omniprésentes (coquillages, cornes animales, limaçon de l'oreille), partout où la nature remplit l'espace de façon régulière et économique. Une spirale utilise un minimum de matière. En se développant elle modifie sa taille mais pas sa forme. La spirale d'or correspond aussi à la disposition des étoiles de plusieurs galaxies dans l'Univers ou encore à celle des formations nuageuses dans les tempêtes, les cyclones et les ouragans.

Ammonite
L'enroulement régulier d'une ammonite se fait suivant une
spirale logarithmique.

La découverte des quasicristaux, de molécules en forme de dodécaèdre (constitué de 12 pentagones), de certains virus ayant cette forme montre que la symétrie d'ordre cinq est assez fréquente dans la nature. Cela augmente l'importance du nombre d'or en science, cependant il reste très loin derrière le nombre π et bien d'autres.

" On doit être chez Fibonacci ! "

voir aussi les liens externes suivants :
géométrie dans la nature
et aussi une vidéo splendide La nature par les nombres


Un Aloés : Aloe polyphylla,

 

SUITE
     

(1)ROBERT VINCENT Géométrie du nombre d'or éditions chalagam
L'art des batisseurs romans association des amis de l'abbaye de Boscodon
CLAUDE JACQUES WILLARD Le nombre d'or éditions Magnard
JEAN-PAUL DELAHAYE Pour la Science Août 1999
ORTOLI WITKOWSKI La baignoire d'Archimède Sciences
Le nombre d'or Que-sais je ?
LUCAS PACIOLI La divine proportion éditions Navarin
MATILA GHYKA Le nombre d'or éditions Gallimard
WARUSFEL Les nombres et leurs mystères éditions du Seuil
D. NEROMAN Le nombre d'or clé du monde vivant Dervy-livres, 6 rue de Savoie, Paris V