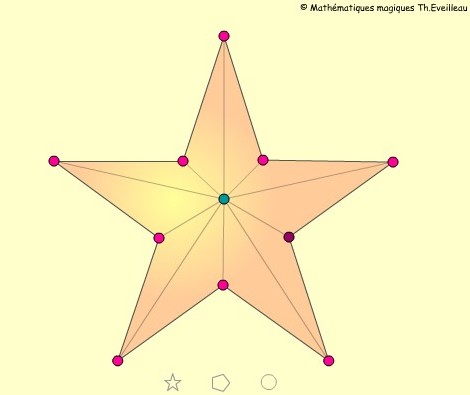
Le
pentagone d'or des compagnons
Une
droite est dite coupée en EXTREME et MOYENNE RAISON
Lorsque la droite entière est à son plus grand segment
ce que
le plus grand segment est au plus petit
EUCLIDE
les éléments
|
|
 Une
construction ancienne du pentagone régulier Une
construction ancienne du pentagone régulier
Nous
allons construire un pentagone régulier par une méthode
venant des Compagnons.
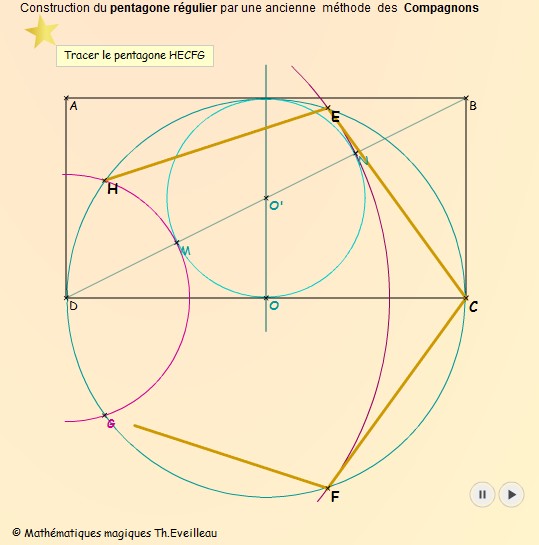
La construction s'effectue à partir d'un rectangle barlong
ABCD de rapport 2 sur 1 (rappelant certaines
travées de nef d'églises gothiques).
AB = 2R et CB = 2r.
Tracer le milieu O d'une longueur et le centre O' du
rectangle.
On trace ensuite le cercle de centre O de rayon R puis
le cercle de centre O' et de rayon r.
Ce dernier cercle coupe la diagonale du rectangle en M
et N.
Les cercles
.de centre D passant par M et
.de centre D passant par N coupent le cercle
de rayon R en H, G, E et F.
Le pentagone HECFG est le pentagone régulier
cherché.
CLIQUER
Démonstration
Choisissons 2R
pour la longueur du rectangle et 2r largeur du rectangle avec
r = R/2.
Dans le triangle rectangle DEC ( inscrit dans
un demi cercle de rayon R), nous avons
DC = 2R et CE²
= DC² - DE²
donc CE² = 4 R² - DE²
or DE = DN = DO' + O'N = DO' + r
Dans le triangle rectangle DOO' nous avons DO'² = OO'²
+ DO² soit DO'² = r² + R²
d'où DO'² = r² + R² = (R/2)² + R²
soit
DO'² = R²/4 + R² = 5R²/4 et
DO' = R/2 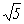
alors DE = DO' + r devient DE = R/2 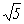 + R/2 soit DE = (1 +
+ R/2 soit DE = (1 + 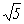 )
R/2 )
R/2
donc CE² = 4 R² - DE² = 4 R² - R²/4 (1
+ 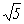 )²
)²
Cela donne CE = R/2 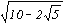
Nous retrouvons HG
= CE =
2 R (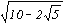 )
/ 4 = 2 R sin (π/5) . )
/ 4 = 2 R sin (π/5) .
Eventuellement, voir la page du triangle d'or pour
retrouver ce résutat.
Il s'agit
donc bien du côté du pentagone régulier.
SUITE

|