Une droite est dite coupée en EXTREME et MOYENNE RAISON
Lorsque la droite entière est à son plus grand segment ce que
le plus grand segment est au plus petit
                                                             EUCLIDE les éléments   

Le triangle d'or

Un triangle d'or est un triangle isocèle d'angles 72°, 72° et 36°.
Le rapport du grand côté sur le petit est égal au nombre d'or.

CLIQUER

La spirale du triangle d'or

Cette spirale est une 'fausse' spirale parce qu'elle est constiutée d'arcs de cercles au lieu d'avoir une variation continue du rayon. Cependant les raccordements des arcs sont parfaits car la condition de tangence est respectée. Les centres des arcs sont à chaque fois situés sur la même droite perpendiculaire à cette tangente.  

 Quelques démonstrations

 Pourquoi le rapport des côtés est-il égal au nombre d'or avec les angles de 36° et 72° ?
La démonstration fait appel aux connaissances du lycée. La mesure des angles ci-dessous est donnée en radians : 72°= 2π/5.
Tout d'abord nous nous servirons du résultat suivant qui est très important pour tout ce qui touche aux pentagones et décagones réguliers :

cos (2π/5) = ( - 1 +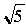) / 4

Ce dernier résultat peut s'obtenir à l'aide des formules de trigonométrie       cos2 (π/5) + sin2 (π/5) = 1       sin (2π/5) = 2cos (p/5).sin (π/5)      cos (2π/5) = 2 cos2(π/5) - 1      sin (a+b) = sina.cosb + sinb.cosa      sin (π-a) = sin(a) Posons X =cos (π/5) et Y=sin (π/5)       X2 + Y2 = 1       sin (2π/5) = 2XY       cos (2π/5)=2X2-1       sin (3π/5) = sin ( π- 2π/5) = sin ( 2π/5) donc 2 X Y = 2cos (π/5).sin (π/5) = sin (2π/5) = sin (π-2π/5)          = sin (3π/5) = sin (2π/5 +π/5 ) = sin (2π/5).cos (π/5) + sin (π/5).cos (2π/5)          = 2 XY.X + Y.(2X2-1) = 2 X2Y + 2X2Y-Y = 4 X2Y -Y d'où 2 X Y = 4 X2Y -Y soit puisque Y non nul :                       4 X2 - 2 X - 1 = 0 dont les racines sont ( 1 +) / 4 et ( 1 -) / 4 La racine positive donne cos (π/5) = ( 1 +) / 4 et cos (2π/5) = 2 cos2(π/5) - 1 soit          cos (2π/5) = ( - 1 +) / 4

Le rapport des côtés du triangle d'or est égal au nombre d'or

Prenons le triangle ABD dont les mesures des angles sont indiquées sur la figure ci-contre. Nous avons la relation trigonométrique : DB2 = AD2 + AB2 - 2 AD.AB.cos 36° DB2 = AD2 (2 - 2 cos 36°) = 2AD2 (1 - cos 36°) (DB/AD)2 = 2 (1 - (1 +) / 4 ) (DB/AD)2 = 2 (3 -) / 4 (DB/AD)2 = ( 3 -) / 2 (AD/DB)2 = 2/ ( 3 -) = 2 ( 3 +) / 4 = ( 3 +) / 2 OR φ2 = ()² = φ + 1 donc φ 2 = ( 3 +) / 2 On en déduit que AD/DB = φ

 

 Une succession de triangles d'or avec la bissectrice ?

Prenons le triangle d'or ABD. B = D = 72° et A = 36° et AD / BD = φ. La bissectrice de l'angle D coupe (AB) en I. Le triangle AID est isocèle et IA = ID Dans un triangle le pied de la bissectrice d'un angle partage le côté sur lequel elle aboutit dans le même rapport que celui des côtés de l'angle qu'elle partage, donc IA / IB = AD / DB = φ et IA / IB = ID / IB = φ Le triangle IDB est donc un triangle d'or et on peut poursuivre le processus indéfiniment.

SUITE
       

(1)ROBERT VINCENT Géométrie du nombre d'or éditions chalagam
L'art des batisseurs romans association des amis de l'abbaye de Boscodon
CLAUDE JACQUES WILLARD Le nombre d'or éditions Magnard
JEAN-PAUL DELAHAYE Pour la Science Août 1999
ORTOLI WITKOWSKI La baignoire d'Archimède Sciences
Le nombre d'or Que-sais je ?
LUCAS PACIOLI La divine proportion éditions Navarin
MATILA GHYKA Le nombre d'or éditions Gallimard
WARUSFEL Les nombres et leurs mystères éditions du Seuil
D. NEROMAN Le nombre d'or clé du monde vivant Dervy-livres, 6 rue de Savoie, Paris V