Quine et nombre d'or

Fibonacci exposa les connaissances mathématiques des Arabes et introduisit l'emploi des chiffres dits 'arabes', il étudia les fractions continues et inventa la suite qui porte son nom actuellement.
Nous avons déjà rencontré la suite de Fibonacci dans les lapins et le morceau caché. Une suite bâtie sur le même principe a été vue dans le prodigieux calcul.
A l'origine Fibonacci (1170-1240) élabora cette suite pour savoir combien de lapins il obtiendrait à la fin de l'année si chaque couple produisait un nouveau couple par mois.
Rappelons que dans cette suite de nombres entiers, chaque nombre est obtenu en ajoutant les deux nombres qui le précèdent : 1       1       2       3       5       8       13       21       34       55       89       144       233 ...

Cette suite a été nommée ainsi par Edward LUCAS au 19^ème siècle.
Le rapport de deux termes consécutifs de la suite tend vers le nombre d'or qui est encadré une fois par excès et une fois pas défaut avec une précision croissante.

La QUINE Son usage est généralisé de l'antiquité au 19ème siècle dans le bassin méditerranéen et en Europe. La quine est la suite de cinq mesures étalonnées sur les dimensions du corps humain. La CANNE des maîtres d'œuvre est l'instrument de mesure des architectes des monuments antiques romans et gothiques, et d' "œuvriers" pratiquant l'art du trait, méthode de tracés et de calculs réalisés avec la règle et le compas. 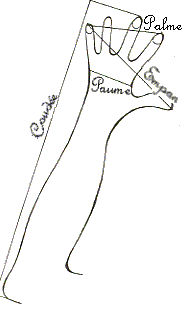Les partages de la QUINE forment une suite additive, chaque dimension est la somme des deux précédentes, comme dans la suite de Fibonacci : COUDEE = PIED + EMPAN                   PIED = EMPAN + PALME                               EMPAN = PALME + PAUME Selon les pays, les époques, les régimes, les religions ou les monuments les mesures de bases étaient différentes mais la progression était semblable.

La COUDEE ROYALE EGYPTIENNE dénommée mesure de l'initié est estimée au 19^ème siècle à 52,36 cm.

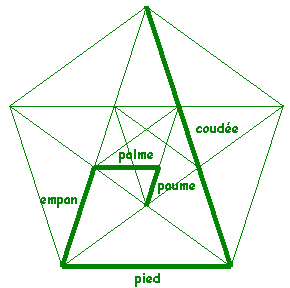
Cette suite est aussi géométrique puisque le rapport entre deux mesures consécutives est le nombre d'or. Nous le visualisons sur la suite des pentagones du schéma de gauche.

Avec des grains d'orge
Outre les dimensions du corps humain, la QUINE aurait aussi comme étalon le grain d'orge "ésotérique" (source bocodienne) dans le sens de la longueur : la LIGNE associée à la suite de Fibonacci.

Léonard de Vinci a  étudié les proportions du corps humain et aurait trouvé une analyse harmonique autour du nombre d'or. Il est évident qu'en choisissant certaines lignes on approchera le nombre d'or.
Evaluer le degré de perfection avec le nombre d'or est inquiétant ! Selon les êtres humains les proportions ne sont pas respectées et la théorie de la beauté basée sur ce nombre est pour le moins étonnante ! (1

Proportions de l'homme parfait de Vitruve : le rapport de AB sur GA est égal au nombre d'or.

L'homme patfait ou l'homme de Vitruve, conservé à l'Académie Royale de Venise. Le quotient entre la mesure du côté du carré et celle du rayon du cercle est le nombre d'or.

Trois rectangles d'or contenant chacun deux rectangles d'or.

SUITE
     

(1)ROBERT VINCENT Géométrie du nombre d'or éditions chalagam
L'art des batisseurs romans association des amis de l'abbaye de Boscodon
CLAUDE JACQUES WILLARD Le nombre d'or éditions Magnard
JEAN-PAUL DELAHAYE Pour la Science Août 1999
ORTOLI WITKOWSKI La baignoire d'Archimède Sciences
Le nombre d'or Que-sais je ?
LUCAS PACIOLI La divine proportion éditions Navarin
MATILA GHYKA Le nombre d'or éditions Gallimard
WARUSFEL Les nombres et leurs mystères éditions du Seuil
D. NEROMAN Le nombre d'or clé du monde vivant Dervy-livres, 6 rue de Savoie, Paris V

(2) Lire la numérologie de Jean-Paul Delahaye Pour la Science Scientific American Août 1999.