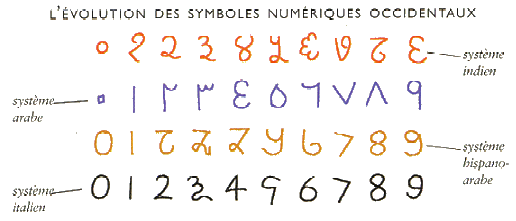|
L'histoire des
mathématiques est précédée d'une longue
préhistoire dont nous avons des traces remontant à 4000
ans. Les animaux supérieurs, les jeunes enfants perçoivent
dans notre monde deux entités abstraites fondamentales : le nombre
et la forme. L'arithmétique et la géométrie furent
ainsi, longtemps distinctes, les deux sciences fondamentales. Au départ
la connaissance des nombres chez l'homme n'est pas très fine.
L'homme, dans les sociétés primitives, ne distingue pas
deux ensembles équipotents, il sait à peine compter :
un, deux, beaucoup. "Beaucoup" se dit "tres" en
latin : ce mot subsiste encore aujourd'hui en français : "très"
mais aussi "trois"!
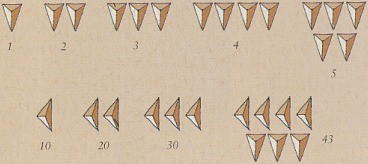
Les plus anciennes civilisations observaient la ronde des astres dans le ciel. Nous savons ainsi que les Sumériens d'Uruk et de Nippur (-3000) utilisaient déjà un calendrier lunaire. Et l'idée leur vint de représenter les nombres par des symboles : la lune représente l'unité et des lunes accolées les nombres suivants. La nécessité de faire des comptes et de les écrire conduit à utiliser des abréviations plus commodes. La barre verticale ou oblique tient lieu alors d'unité (phénicien, Syriaque, Nabatéen, Grec ancien, Sudarabique, Indien). Les ensembles de cinq, dix ou vingt unités sont abrégés par des symboles spéciaux éventuellement dérivés de leur nom. Tous ces systèmes sont additifs, c'est-à-dire que le nombre codé est la somme des symboles représentés.
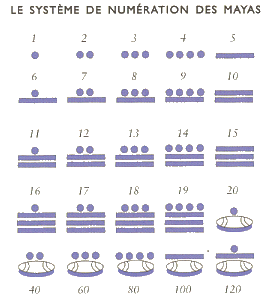
Les Babyloniens (-2000) se distinguent en inventant le système
sexagésimal : les symboles de base valent 1, 10, 60, puis 600,
3600, 36000 et ainsi de suite. Ce système s'est perpétué
jusqu'à nous, par l'astronomie, pour les mesures sexagésimales
de temps et d'angle.
Une tablette d'argile babylonienne ayant 3700 ans a été identifiée comme la table trigonométrique la plus ancienne et la plus précise au monde. Ceci parce que le système sexagésimal possède des fractions plus exactes qu'un système décimal. Les Babyloniens auraient ainsi devancé les anciens grecs de 1000 ans avec l'invention de la trigonométrie ! 
Plusieurs civilisations
ont de plus, l'idée d'utiliser les lettres de leur alphabet pour
représenter les nombres. Ceci permet de donner un sens à
certains d'entre eux : ce sont les calculs cabalistiques. Le nombre
correspondant à une lettre devient fonction de la position de
celle-ci dans le mot ; la nécessité de marquer le "rien"
se fait sentir. L'origine du zéro reste toutefois obscure. Il
existe de façon sûre dans des textes indiens du VIème
siècle où il prend la forme d'un point. Dans des écrits
astronomiques grecs, le zéro est représenté par
la lettre o initiale du mot grec omdem
: "rien". La
forme actuelle de nos chiffres, notre système décimal,
vient donc de l'Inde de l'Ouest, par l'intermédiaire des Arabes.
Mais ce n'est guère qu'au XIIIème siècle qu'elle
pénétra en Italie, adoptée par les commerçants
de Florence. Son emploi n'est généralisé qu'au
XVIème siècle.
C'est l'invention de l'imprimerie (1440), qui fixe finalement la forme de ces dix symboles. L'usage de la virgule pour noter les nombres "réels" ne se répand qu'au XVIIème siècle. Les
quatre opérations sont déjà connues des Egyptiens.
Voici la multiplication égyptienne de 37 par 24 : (pour plus d'explications voir la multiplication égyptienne )
Mais
leurs représentations sont souvent malcommodes.
La juxtaposition marque l'addition et un y retourné marque chez les grecs, la soustraction. Finalement,
ce sont les copistes du Moyen-Age qui abrègent puis déforment
le mot "et", qui devient "+", tandis que l'habitude
de séparer dans les comptes le poids de la tare à l'aide
d'un tiret horizontal donne naissance au signe "-". Les signes
"+" et "-" apparaissent dans l'Arithmétique
commerciale de Widmann en 1489. Les signes de multiplication et
de division actuels ne sont introduits qu'au XVIIème siècle.
L'égalité est marquée en Europe au XVIIème
siècle par le symbole
 par
lequel les astronomes désignent la constellation du Taureau.
mais le mot latin "aequalis" en toutes lettres se rencontre
aussi, il est progressivement abrégé en æ et devient,
finalement, le signe "=". Il semble avoir été
inventé par le mathématicien anglais Robert Recorde (1510-1558),
professeur à Oxford et à Londres. Le symbole
désigne alors le nombre 1000. C'est
J. Wallis qui, vers 1660, l'élève au rang "d'infini"
; auparavant, cette notion d'infini n'avait pas d'existence.Conclusion
L'humanité a mis plusieurs millénaires pour domestiquer le nombre et la science n'est ce qu'elle est que depuis quelques siècles ! Les mathématiques ne se sont pas faites en un jour et, qui plus est, leur enfance n'est guère éloignée de nous. Quoi d'étonnant dès lors, puisque les hommes ont mis si longtemps à représenter les nombres et les opérations, à ce qu'un écolier rencontre à ce propos quelques difficultés ?
(1) |
vaut 1 unité.
vaut 10 unités .
vaut 100 unités.
1000 unités. 