Nous ne possédons, malheureusement, que fort peu de détails sur la vie d' Abû Jacfar Muhammad bin Mûsâ al-Khuwârizmî . Nous ignorons tout de sa parentèle. Son nom, cependant, nous apprend qu'il était originaire d'une province persane relativement excentrée du Dâr Al-Islâm(1) car sise au Nord de l'Iran actuel, en Asie Centrale : l'antique Choresmia(2) . Celle-ci, de nos jours, est partagée entre l'Ouzbékistan, le Turkménistan et la Karakalpakie.

Nous savons également qu'il vécut dans la première moitié du IX^e siècle de l'ère chrétienne, vraisemblablement entre 800 et 847⁽³⁾. Il fut donc rappelé à Dieu avant l'âge de cinquante ans. Cet homme a accompli en moins d'un demi-siècle ce que d'autres ne feront jamais, même en vivant centenaire.
       Qui était Al-Khuwârizmî ? Un savant. Certes, mais encore. Un génie, de toute évidence. Mais ne fut-il pas davantage ? Assurément ! Notre héros brilla, et avec quel éclat, dans cinq domaines qui en firent un remarquable compagnon des sciences. En effet, ce Persan d'expression arabe fut tout à la fois astrologue, astronome, géographe, historien et surtout mathématicien. L'étendue de ses travaux dans l'art du calcul ouvrirent la voie à d'extraordinaires progrès. Et désormais, quand nous volons dans les cieux nous le lui devons en grande partie. Si nous guérissons tellement de maladies et reculons d'autant le moment où Thanatos, après avoir arraché une boucle de cheveux à un malheureux mortel l'emporte au-delà de l'Achéron, nous pouvons l'en remercier. Lorsque nous nous émerveillons, à juste titre, des fascinantes possibilités des ordinateurs (qui ne sont pourtant que des arithmographes perfectionnés), nous en sommes toujours redevables à ce Persan. Car à l'origine de ces miracles et de tous les prodiges qui ont façonné les technologies modernes, il y a un métier féerique tout en subtilités, en formules magiques et en courbes séduisantes. C'est celui d'architecte des chiffres. Seul le mathématicien est inspiré comme le poète. Avec des vers, l'un nous emmène dans un rêve ; l'autre transmue le songe enchanteur en réalité virtuelle avant d'en faire une évidence tout à fait concrète. Souvenons-nous, les Grecs imaginèrent des ailes de cire pour le fils de Dédale tandis que Clément Ader transforma chacun d'entre nous en Icare triomphant. Du désir à sa réalisation, il n'y a souvent que l'art du calcul.

Si la vie d'Abû Ja^cfar Muhammad bin Mûsâ al-Khuwârizmî, faute de témoignages, demeure assez obscure, son œuvre, en revanche, est bien connue. Ses écrits ont, pour l'essentiel, été conservés et, mieux encore pour l'Occident, promptement traduits en latin après leur introduction chez les Maures d'Al-Andalus⁽⁴⁾. Mais, à présent, jouons-nous de Chronos et immobilisons sa faux pour remonter le cours du temps d'environ onze cents ans.

 

    

 

 

 

 

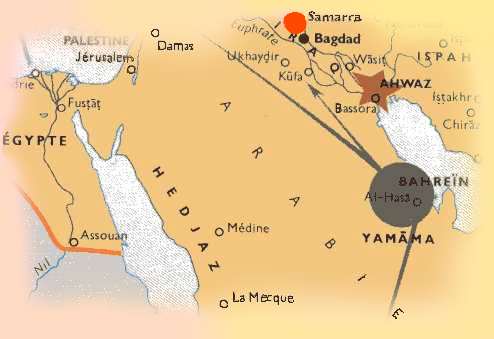
'Abassides au VIIIe et IXe s.

 

 

A l'époque qui nous intéresse, la ville ronde de Bagdad, capitale de l'Empire abbasside, est dirigée par un prince éclairé répondant au nom d'Al-Ma'mûn⁽⁵⁾. Celui-ci, pour succéder à son père - le célèbrissime Hârûn Ar-Rachîd -, a dû guerroyer et intriguer contre ses deux frères. Une fois parvenu au faîte de la puissance, le nouveau calife ne se contente pas d'accroître les possesssions de ses Etats, faire respecter l'ordre, rentrer force dinars et dirhams dans les coffres du Bayt Al-Mâl⁽⁶⁾. Bien plus qu'un roi, ce monarque, est un érudit, un philosophe avisé. C'est aussi un original. Ainsi, un jour, l'idée lui vint de bâtir un édifice afin d'y rassembler tous les écrits scientifiques découverts dans l'empire. Cet édifice est baptisé Bayt Al-Hikmah, c'est-à-dire "Maison de la Sagesse". L'Abbasside y mande aussitôt les meilleurs mathématiciens, géographes, médecins, poètes et traducteurs du royaume. Il leur confie tous ses grimoires (parmi lesquels se trouvent quantités de textes grecs perdus ou ignorés en Europe), à charge pour eux de les étudier, bien traduire et d'en tirer la substantifique moelle. Au crédit des savants qui animent le Bayt Al-Hikmah, outre une liste impressionnante de traductions de textes scientifiques araméens, grecs et même sanscrits, il faut porter la mesure d'un degré du méridien⁽⁷⁾ terrestre et de nombreuses observations astronomiques.

       C'est sur l'invitation d'Al-Ma'mûn, croit-on, qu'Abû Ja^cfar Muhammad bin Mûsâ al-Khuwârizmî quitte, encore jeune, sa Chorasmie natale pour venir exercer ses talents dans la "Maison de la Sagesse". C'est dans le cadre très studieux de cet établissement, d'un genre tout à fait inédit, que le savant persan donne toute la mesure de son génie et qu'il rédige, très vraisemblablement, l'essentiel de son œuvre. Celle-ci comprend un peu plus d'une dizaine d'ouvrages, parmi lesquels il faut signaler une Algèbre, en fait la première de l'histoire sur laquelle nous allons revenir, une Arithmétique, une Classification des sciences, des Tables astronomiques, une Géographie, une Etude sur le calendrier juif, deux traités sur l'Astrolabe, une Chronique et un manuel sur les Cadrans solaires.

       Arrêtons-nous, quelques instants, sur une autre de ses œuvres, le Livre de la Configuration de la Terre. Il le rédige en collaborant, sur l'instance du calife, avec des collègues géographes à la création d'une mappemonde. Réfléchissant, pour ce faire, sur l'œuvre de Ptolémée, il apporte un certain nombre de retouches à l'Almageste, notamment en le corrigeant sur la longueur excessive de la Méditerranée. Il complète aussi l'ouvrage du polygraphe alexandrin en ajoutant aux villes de l'Antiquité gréco-latine les cités et accidents géographiques du jeune empire musulman. Cette géographie gagne en précision sur la précédente. C'est très appréciable pour la connaissance de la péninsule Arabique et de la Perse, deux contrées relativement méconnues par Athènes et Rome.

       Mais c'est surtout dans le domaine des mathématiques qu'Al-Khuwârizmî innove. Il fait paraître, entre 813 et 830, un traité qui révolutionne la science des nombres. Celui-ci est peut-être pour partie, suscité par une lecture toute récente des Eléments d'Euclide que vient de traduire en arabe l'un de ses collègues à la "Maison de la Sagesse", le mathématicien Al-Hajjâj ibn Matar. Le livre s'intitule Kitâb al-mukhtaçar fî hisâb al-jabr wa-l-muqabâlah ce que l'on peut rendre par Précis de calcul par réduction et comparaison. L'algèbre vient de naître.
      De quoi s'agit-il ? Tout simplement, comme le titre l'indique, de résoudre des problèmes de calcul par réduction (jabr en arabe) et "comparaison" (muqabâlah en arabe) de manière à obtenir des équations dont la résolution est considérablement simplifiée. De la sorte, les mathématiques gagnent tant en clarté, dans le raisonnement, qu'en rapidité, dans l'exécution des opérations.

 

Exemple 8 x2 - 4 x + 6 = 6x2 + 4 par al-jabr :        8 x2 + 6 = 6x2 + 4x + 4                         Les termes négatifs, sont acceptés mais on préfère s'en débarrasser. par al-hatt :         4x2 + 3 = 3x2 + 2x + 2                         On a divisé les deux membres par un même nombre. par al-muqâbala : x2 + 1 = 2x                         On a réduit les termes semblables de part et d'autre.   L'équation est réduite à l'une des formes canoniques d'al-Khuwârizmî

Dans l'expression hisâb al-jabr wa-l-muqabâlah "calcul par réduction et comparaison", un mot est promis à une singulière destinée : jabr qui signifie "réduction". Muni de l'article al, il appartient au vocabulaire médical et s'entend plus spécifiquement comme une technique chirurgicale visant à la "réduction - au sens de réparation - d'un membre démis". Le traité d'al-Khuwârizmî est traduit en latin, au XII^e siècle, par Robert de Chester (Liber Algebrae et Almucabola) et Gérard de Crémone (De jebra et almucabola) de l'Ecole de Tolède. De là, il se latinise en algebra, substantif dont sont issus les calques des autres langues européennes Ainsi en français, le mot "algèbre" est attesté à la fin du XIV^e siècle. A cette époque, et jusqu'aux travaux du mathématicien François Viète⁽⁸⁾, l'algèbre englobe également l'arithmétique⁽⁹⁾. En castillan, si le terme d'algebra, sous l'acception de parte de las matematicas est l'aboutissement, en 1604, du même cheminement que son équivalent français, il faut rappeler que dès 1495 - soit plus d'un siècle plus tôt - il se définit comme "l'art de remettre à leur place les os disloqués", un sens éminemment plus proche de l'étymon arabe. De même facture, évoquons les campagnes espagnoles, qui naguère, possédaient chacune leur algebrista guérissant foulures et fêlures, réduisant fractures et remettant tout membre fracassé selon les règles de l'art quasi magique des rebouteurs. Aujourd'hui, dans les langues de Cervantès et Molière, ce type de guérisseur s'est effacé devant le spécialiste des formules de calcul : l'algébriste.

 

                               

 

 

 

 

 

 

 

  

Nonobstant, l'influence d'Abû Ja^cfar Muhammad Mûsâ al-Khuwârizmî ne s'arrête pas à la découverte d'une nouvelle branche des mathématiques.

	En effet, le savant exerce, au travers des siècles, un tel ascendant sur les lettrés médiévaux que ces derniers s'approprient son nom pour désigner tout procédé de calcul utilisant les chiffres dits arabes(10), chiffres - comprenant le zéro inconnu alors en Europe - qu'ils découvrent dans les textes provenant du monde islamique.
L'introduction de ces nouveaux signes, surtout pour le maniement des grands nombres, va prodigieusement faciliter les calculs rendus malaisés, voire impossibles avec les chiffres romains(11).

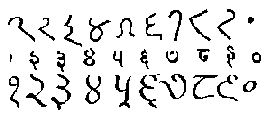
Lorsqu'ils font des opérations à l'aide des "numéros" arabes, nos érudits du XIII^e siècle les baptisent alguarismo en espagnol et augorisme ou algorisme en français. Naturellement ces mots possèdent de nombreuses variantes mais toutes proviennent de la déformation du nom du Persan et désignent l'art de compter avec les chiffres des "Sarrasins". Le latin médiéval, langue des sciences, sous l'influence du mot arithmetica (d'origine grecque), crée la forme algorithmus d'où le français moderne a tiré "algorithme".

        Maintenant que nous savons ce qu'est l'algèbre ne nous effrayons pas devant cette nouvelle et fantastique créature que les mathématiciens ont appelé "algorithme". N'avons-nous pas déjà expliqué que l'architecte des chiffres et le poète sont de la même essence ? N'est-ce donc pas le moment de laisser l'un de nos chantres s'exprimer ?

Ecoutons Nicolas Boileau :

"Ce que l'on conçoit bien s'énonce clairement."

        Très jolie formule que l'on peut appliquer à un algorithme qui, dans sa plus simple expression, n'est rien d'autre que la décomposition d'un calcul en une suite d'opérations arithmétiques.

        Illustrons notre propos avec l'algorithme d'Euclide. Celui-ci, exposé au livre VII des Eléments, explique comment obtenir le plus grand commun diviseur (PGCD) entre deux nombres donnés en procédant par divisions successives.

Principe : tout diviseur commun à deux nombres, divise le plus petit des deux et le reste de la division du plus grand par le plus petit. Soit par exemple le calcul du PGCD de1680 et 231 1680 = (231 x 7) + 63    Le PGCD divise 231 et 63 231 = (63 x 3) + 42       Le PGCD divise 63 et 42 63 = (42 x 1) + 21         Le PGCD divise 42 et 21 42 = (21 x 2) + 0    Le PGCD est 21 car c'est le dernier reste non nul.

 

         On se souvient de la célèbre apostrophe d'un Parisien dans le roman de Montesquieu⁽¹²⁾,

"Comment peut-on être Persan ?".

         Mais, après avoir entr'aperçu toute cette magie des nombres grâce à al-Khuwârizmî, demandons-nous :

Comment ne pas être Persan ?

         Bien plus encore :

Comment ne pas être algébriste ?

 

  

Sources :
Histoire universelle des chiffres de Georges Ifrah éditions Robert Laffont 
Vie et œuvre des grands mathématiciens de Jean-Louis Audirac éditions Magnard
Mathématiques et mathématiciens de Jean Itard éditions magnard