¿Cómo no ser persa?

texto de Emmanuel H. de BRYE-DONNELLY
con el agradecimiento al
Profesor Jean-Loup Motchane (P.U. Paris VII)

Este texto ha sido publicado en

- LES CAHIERS DE L'ORIENT 1er trimestre 1998                                                   - LE BULLETIN DE l'ASSOCIATION DES ANCIENS ELEVES DE L'INALCO abril 1998

 

No poseemos, desgraciadamente, más que  muy pocos  detalles sobre la vida de Abû Jacfar Mohammad bin Mûsâ al-Juârizmî . Ignoramos todo de su parentela. Su nombre, sin embargo, nos dice que era originario de una provincia persa relativamente alejada del Dâr Al-Islâm(1) pues estaba situada al Norte del Irán actual, en Asia Central: la antigua Juârizm(2). En la actualidad, ésta se encuentra repartida entre Uzbekistán, Turkmenistán y Karakalpacia.

Sabemos igualmente que vivió en la primera mitad del siglo IX de la era cristiana, presumiblemente entre el 800 y el 847⁽³⁾. Así pues murió antes de la edad de cincuenta años. Este hombre realizó en menos de medio siglo lo que otros no  hicieron nunca, incluso viviendo cien años.
¿Quién era Al-Juârizmî?. Un sabio. Ciertamente, pero aún era más. Un genio, evidentemente. ¿Pero no fue algo más?. ¡Seguramente!. Nuestro héroe brilló en cinco dominios, y con tal destello, que hicieron de él un excelente compañero de las ciencias. En efecto, este Persa de expresión árabe fue todo a la vez, astrólogo, astrónomo, geógrafo, historiador y sobre todo matemático. La extensión de sus trabajos en el arte del cálculo abrieron el camino de extraordinarios progresos. Y en adelante, cuando volamos por los cielos se lo debemos en gran parte a él. Si nos curamos en tantas ocasiones de enfermedades y retrocedemos tanto cuando Thanatos, después de haber arrancado un mechón de cabello a un pobre mortal lo lleva junto al Aqueronte, podemos agradecérselo a él. Cuando nos maravillamos, con toda razón, de las fascinantes posibilidades de los ordenadores (que no son sin embargo más que unos aritmógrafos perfeccionados), se lo debemos siempre a este Persa. Pues en el origen de estos milagros y de todos los prodigios que han dado lugar a las tecnologías modernas, existe todo un maravilloso oficio en subtítulos, en fórmulas mágicas y en seductoras curvas. Fue el arquitecto de las cifras. Solamente el matemático está inspirado como el poeta. Con sus versos, uno nos lleva a un sueño; el otro transmuta el ensueño encantador en realidad virtual antes de hacer de ello una evidencia totalmente concreta. Acordémonos de los Griegos, que imaginaron unas alas de cera para el hijo de Dédalo, mientras que Clemente Ader nos transformó a cada uno de nosotros en Ícaro triunfante. Del deseo a su realización, a menudo no existe más que el arte del cálculo.

Si la vida de Abû Ja^cfar Mohammad bin Mûsâ al-Juârizmî, carece de testimonios, permanece bastante oscura, su obra en cambio es muy conocida. Sus escritos, en lo esencial, han sido conservados y, mucho mejor para Occidente, traducidos pronto al latín, tras su introducción entre los Moros de Al-Andalus⁽⁴⁾. Pero, actualmente, burlémonos de Chronos e inmovilicemos su guadaña parar remontarnos por el hilo del tiempo unos mil cien años.  

    

 

 

 

 

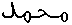
Abásidas en los siglos VIII y IX.

 

En la época que nos ocupa, la ciudad de Bagdad, capital del Imperio abásida, estaba dirigida por un príncipe iluminado, que respondía al nombre de Al-Ma'mûn⁽⁵⁾. Éste, para suceder a su padre -el celebérrimo Hârûn Ar-Rachîd, el de las Mil y una noches-, tuvo que guerrear e intrigar contra sus dos hermanos. Una vez alcanzado el poder, el nuevo califa no se contentó con acrecentar las posesiones de sus Estados, hacer respetar el orden e ingresar inmensas cantidades de dinares y dirhams en los cofres del Bayt Al-Mâl⁽⁶⁾. Más que un rey, este monarca, fue un erudito, un filósofo avispado. También fue un extravagante. Así, un día, le vino la idea de edificar un edificio con el fin de guardar en él todos los escritos científicos descubiertos en el imperio. Este edificio fue bautizado con  Bayt Al-Hikmah, es  decir "Casa de la Sabiduría". La Abásida hace venir allí enseguida a los mejores matemáticos, geógrafos, médicos, poetas y traductores del reino. Les confía todos sus escritos (entre los que se encuentran grandes cantidades de textos griegos perdidos o ignorados en Europa), para que se encarguen de estudiarlos, de traducirlos y de sacar de ellos lo más substancioso. A la lista de sabios que animan el Bayt Al-Hikmah, además de una lista impresionante de traducciones de textos científicos araméos, griegos e incluso sánscritos, hay que añadir la medida de un grado del meridiano⁽⁷⁾ terrestre y numerosas observaciones astronómicas.

Se cree que fue por invitación de Al-Ma'mûn, como Abû Ja^cfar Muhammad bin Mûsâ Al-Juârizmî , siendo todavía muy joven, dejó su Juârizm natal para ir a ejercer sus talentos a la "Casa de la Sabiduría". Y en el muy estudioso marco de este lugar, de un género completamente inédito, es donde el sabio persa da toda la medida de su genio y donde redacta, muy presumiblemente, lo esencial de su obra. Ésta comprende poco más de una decena de obras, entre las cuales hay que señalar un Álgebra, de hecho la primera de la historia, sobre la que volveremos, una Aritmética, una Clasificación de las ciencias, unas Tablas astronómicas, una Geografía, un Estudio sobre el calendario judío, dos tratados sobre el Astrolabio, una Crónica y un manual sobre los Cuadrantes solares.

Detengámonos, algunos instantes, sobre otra de sus obras, el Libro de la Configuración de la Tierra. Lo redacta en colaboración, y a instancias del califa, con  colegas geógrafos para la creación de un mapamundi. Reflexionando, para su realización, sobre la obra de Ptolomeo, aporta un cierto número de retoques al Almagesto, corrigiendo notablemente la longitud excesiva del Mediterráneo. Completa también la obra del polígrafo alejandrino añadiendo a las ciudades de la Antigüedad greco-latina las ciudades y accidentes geográficos del joven imperio musulmán. Esta geografía gana en precisión sobre la precedente. Es muy apreciable para el conocimiento de la península Arábiga y de Persia, dos regiones relativamente desconocidas por Atenas y Roma.

Pero es sobre todo en el dominio de las matemáticas donde innovó Al-Juârizmî . Publica, entre el 813 y el 830, un tratado que revoluciona la ciencia de los números. Éste se debe quizá al interés suscitado en una lectura  reciente de los Elementos de Euclides, que acaba de traducir al árabe uno de sus colegas en la "Casa de la Sabiduría", el matemático Al-Hajjâj ibn Matar. El libro se titula Kitâb al-mukhtaçar fî hisâb al-jabr wa-l-muqabâlah,  lo que se puede tomar por Compendio de cálculo por reducción y comparación. El álgebra acaba de nacer.

¿De qué se trata?. Simplemente, como indica el título, de resolver problemas de cálculo por "reducción" (jabr en árabe) y "comparación" (muqabâlah en árabe), del modo de obtener ecuaciones cuya resolución está considerablemente simplificada. De tal suerte, los matemáticos ganan tanto en claridad, en el razonamiento, como en rapidez, en la ejecución de las operaciones.

 

Ejemplo 8 x2 - 4 x + 6 = 6x2 + 4 por al-jabr :        8 x2 + 6 = 6x2 + 4x + 4                         Los términos negativos están aceptados, pero prefieren deshacerse de ellos. por al-hatt :         4x2 + 3 = 3x2 + 2x + 2                         Se han dividido los dos miembros por un mismo número. por al-muqâbala : x2 + 1 = 2x                         Se han reducido los términos semejantes de una parte y de la otra.   La ecuación está reducida a una de las formas canónicas de al-Jwârizmî

En la expresión hisâb al-jabr wa-l-muqabâlah "cálculo por reducción y comparación", una palabra está comprometida para un singular destino: jabr que significa "reducción". Provista del articulo al, pertenece al vocabulario médico y se refiere más específicamente a una técnica quirúrgica dirigida a la "reducción -en sentido de reparación- de un miembro dislocado". El tratado de Al-Juârizmî se tradujo al latín, en el siglo XII, por Roberto de Chester (Liber Algebrae et Almucabola) y Gerardo de Cremona (De jebra et almucabola) de la Escuela de Toledo. De ahí se latiniza en álgebra, sustantivo del que provienen las copias de las otras lenguas europeas. Así en francés, la palabra "algèbre" está certificada a finales del siglo XIV. En esta época, y hasta los trabajos del matemático François Viète⁽⁸⁾, el álgebra incluye también a la aritmética⁽⁹⁾. En castellano, si el término de álgebra, bajo la acepción de parte de las matemáticas es el resultado, en 1604, del mismo camino seguido que su equivalente francés, hay que recordar que desde 1495 -o sea desde hace más de un siglo- se define como "el arte de volver a poner en su sitio los huesos dislocados", un sentido eminentemente más próximo al etimológico árabe. Del mismo modo, si evocamos las campañas militares españolas, no hace mucho que poseían cada una su algebrista, que curaba esguinces y fisuras, reduciendo fracturas y volviendo a colocar todo miembro roto según las reglas del arte cuasi mágico de los ensalmadores. Hoy en día, en las lenguas de Cervantes y Molière, ese tipo de curandero ha desaparecido ante el especialista de las fórmulas de cálculo: el algebrista.

 

                               

 

 

 

 

 

 

 

  

No obstante, la influencia de Abû Ja^cfar Muhammad Mûsâ Al-Juârizmî no se detiene en el descubrimiento de una nueva rama de las matemáticas.

	En efecto, el sabio ejerce, a través de los siglos, un ascendente tal sobre las letras medievales que éstas se apropian de su nombre para designar a todo procedimiento de cálculo utilizando las cifras que se dicen árabes(10), cifras -que comprenden el cero, desconocido por aquel entonces en Europa- que descubren en textos provenientes del mundo islámico.
La introducción de estos nuevos signos, sobre todo para el manejo de los grandes números, va a facilitar prodigiosamente  los cálculos que se vuelven enfermos, véase imposibles, con las cifras romanas(11).

Cuando hacen operaciones con  ayuda de los "números" árabes, nuestros eruditos del siglo XIII  los bautizan con guarismo en español y augorisme o algorisme en francés. Naturalemente estas palabras poseen numerosas variantes, pero todas provienen de la deformación del nombre del Persa, y designan al arte de contar con las cifras de los "Sarracenos". El latín medieval, lengua de las ciencias, bajo la influencia de la palabra arithmetica (de origen griego), crea la forma algorithmus, de donde en francés y en español modernos se ha sacado "algorithme" y "algoritmo".

 Ahora que sabemos lo que es el álgebra, no nos asustemos ante esta nueva y fantástica criatura que los matemáticos han llamado "algoritmo". ¿No hemos dicho ya que el arquitecto de las cifras y el poeta son de la misma esencia?, ¿no es pues el momento de dejar expresarse a uno de nuestros cantores?

Ecuchemos a Nicolás Boileau :

"Lo que se piensa bien se expresa con claridad"

Una fórmula muy bonita que se le puede aplicar a un algoritmo que, en su expresión más simple, no es otra cosa que la descomposición de un cálculo en una sucesión de operaciones aritméticas.

Ilustremos nuestro propósito con el algoritmo de Euclides. Éste, expuesto en el libro VII de los Elementos, explica como obtener el máximo común divisor (MCD) de dos números dados procediendo por divisiones sucesivas.

Principio : todo divisor común de dos números, divide al más pequeño de los dos y al resto de la división del más grande entre el más pequeño. Realicemos, por ejemplo, el cálculo del MCD de 1680 y  231 1680 = (231 x 7) + 63    El MCD divide a  231 y a 63 231 = (63 x 3) + 42       El MCD divide a  63  y  a  42 63 = (42 x 1) + 21         El MCD divide a  42  y  a  21 42 = (21 x 2) + 0    El  MCD  es  21, pues es el último resto no nulo.

 

Nos acordamos de la célebre frase de un Parisino en la novela de Montesquieu⁽¹²⁾, "¿Cómo se puede ser Persa?"

Pero, tras  haber percibido toda esta magia de los números, gracias a      Al-Juârizmî, podemos preguntarnos: ¿Cómo no ser Persa?

 Y más aún:

¿Cómo no ser algebrista?

Fuentes :
Historia universal de las cifras de Georges Ifrah. Editorial. Espasa Calpe 
Vie et œuvre des grands mathématiciens de Jean-Louis Audirac, éditions Magnard
Mathématiques et mathématiciens de Jean Itard, éditions magnard