| Pas
de deux sur un damier (suite et fin)
Jeu sur une ou deux lignes
Le
jeu (jeu
de Nim généralisé sur un damier )
Dans le jeu précédent, on
pouvait jouer que sur une seule ligne.
Cette fois on peut jouer en utilisant
une ou deux lignes.
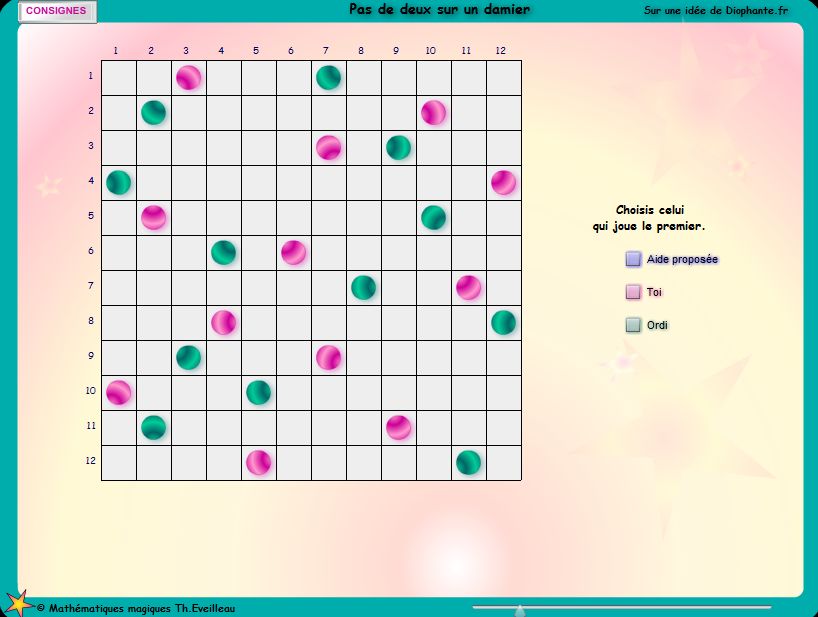
On dispose d'un damier de dimensions 12 x 12 sur lequel des pions roses
et verts ont été placés :
un pion rose et un pion vert sur chacune des 12 rangées.
Leur disposition est aléatoire lorsqu'on REJOUE.
Votre adversaire est l'ordinateur : Ordi
et vous jouez à
tour de rôle.
Vous déplacez les pions roses et
l'ordinateur les verts, dans une
rangée OU dans deux rangées à la fois.
Les pions vont sur n'importe quelle case libre de la rangée vers
la gauche ou vers la droite,
mais sans sauter par-dessus le pion adverse.
Celui qui bloque tous les pions de l'adversaire est le gagnant.
-Choisir d'emblée celui qui joue le premier.
-Ensuite jouer à tour de rôle.
Vous jouez en cliquant-déplaçant les pions avec la souris.
Le curseur en bas de l'animation permet de modifier la vitesse de déplacement
des boules vertes.
ATTENTION l'ordinateur utilise une stratégie efficace et s'il
joue en premier, le bouton AIDE peut devenir inefficace ;).
Si éventuellement vous avez demandé une AIDE au départ,
celle-ci sera visible en glissant la souris sur le bouton AIDE.
ATTENTION, Ordi et ne pardonne aucune erreur d'inattention !
CLIQUER
ANALYSE du jeu
: comment gagner
Ce
jeu rappelle le jeu de Marienbad
simple ou généralisé.
C'est aussi une variante du jeu ayant la même présentation
dans
lequel on pouvait jouer que sur une seule ligne ICI.
La stratégie repose sur la Nim-addition du nombre d'espaces
entre les pions dans chaque chaque rangée.
Les nombres binaires sont éventuellement complétés
avec des zéros à gauche de façon à ce
qu'ils aient tous la même longueur.
Nous additionnons ces nombres binaires en base trois sans retenue
:
0+0 =0 ; 1+1 = 2; 1+0=1 ; 0+1=1 ; 2+1 =0; 1+2 =0;
2+2=1.
Je vais appeler ter-addition cette opération.
Il faut laisser à l'adversaire une situation pour laquelle
la ter-addition des nombres d'espaces entre
deux pions, sera nulle donc PERDANTE.
En effet
en un ou deux coups une situation avec ter-addition
nulle donne toujours une situation avec ter-addition
non nulle GAGNANTE.
Exemple avec la situation proposée au
départ
3 espaces, 7 espaces,
1 espace, 10 espaces, 7
espaces, 1 espace, 2 espaces,
7 espaces, 3 espaces,3
espaces, 6 espaces, 5 espaces.
3
s'écrit 11 en binaire.
7 s'écrit 111 en binaire.
1 s'écrit 1 en binaire.
10 s'écrit 1010 en binaire.
7
s'écrit 111 en binaire.
1 s'écrit 1 en binaire.
2 s'écrit 10 en binaire.
7
s'écrit 111 en binaire.
3 s'écrit 11 en binaire.
3 s'écrit 11 en binaire.
6 s'écrit 110 en binaire.
5 s'écrit 101 en binaire.
La ter-addition de ces nombres donne 0011+0111+0001+1010+0111+0001+0010+0111+0011+0011+0110+0101=1200
Situation non nulle gagnante.
L'ordinateur (pion vert) peut donc jouer ligne 4 colonne 4, puis
ligne 6 colonne 5, ce qui laissera :
3 espaces, 7 espaces,
1 espace, 7 espaces,
7 espaces, 0 espace,
2 espaces, 7
espaces, 3 espaces,3 espaces,
6 espaces, 5 espaces.
3
s'écrit 11 en binaire.
7 s'écrit 111 en binaire.
1 s'écrit 1 en binaire.
7 s'écrit 111 en binaire.
7
s'écrit 111 en binaire.
0 s'écrit 0 en binaire.
2 s'écrit 10 en binaire.
7
s'écrit 111 en binaire.
3 s'écrit 11 en binaire.
3 s'écrit 11 en binaire.
6 s'écrit 110 en binaire.
5 s'écrit 101 en binaire.
La Nim-addition de ces nombres donne 011+111+001+111+111+000+010+111+011+011+110+101=000
On a transformé la situation proposée en situation
nulle PERDANTE pour l'adversaire.
Ce n'est d'ailleurs pas la seule solution (voir
l'AIDE).
Le premier coup de cette situation
est GAGNANT.
Quelquefois,
il existe plusieurs solutions pour jouer et gagner.
A vous de déterminer la meilleure solution qui va terminer
le jeu le plus rapidement possible.
C'est ce que réalise Ordi
dès qu'il le peut ;)
Retrouvez d'autres explications sur ce jeu avec Diophante.fr :
pas de deux sur un damier.
|
