Les pentagones paveurs (1)
Le pavage de Marjorie Rice
Le pavage de Marjorie Rice
De façon générale, on ne peut pas paver le plan avec un pentagone quelconque,
pas plus d'ailleurs qu'avec un pentagone régulier.
Cependant on peut paver avec certains pentagones irréguliers particuliers.
ll existe différents types de pavages,
14 types de pavages pentagonaux avec des pentagones convexes étaient connus jusqu'en 2015.
Une équipe de trois mathématiciens de l'université de Washington Bothell vient de découvrir un quinzième type à l'aide de code informatique.
On ignore si la liste est complète.
Celui-ci de type R2 fut découvert en 1976 par Marjorie Rice.
Femme au foyer, mère de 5 enfants, elle travaillait sur sa table de cuisine
lorsqu'elle découvrit de nombreuses formes géométriqes nouvelles que les professeurs pensaient impossibles.
Depuis, elle a découvert 58 sortes de pavés pentagonaux, pour la plupart inconnus jusque-là.
Son diplôme le plus élevé était un baccalauréat de 1939, pour lequel elle n'avait pris qu'un cours de maths général
(source : Oh, les Nombres ! Clifford A.Pickover Dunod).
Pour paver le plan, les transformations utilisées sont des rotations d'un demi-tour (180°) et autres rotations, des symétries axiales et des translations.
voici comment l'on construit le motif de Marjorie Rice. Il suffit d'une règle et d'un compas.
OC est de longueur arbitraire.
Pour faire tourner le triangle ACD,
il suffit de reporter le segment AD en AF avec F sur(OC),
puis on termine le triangle avec GF= AD et AG = AC.
CLIQUER
On démontre facilement que ce pentagone a 4 côtés de même mesure.
En effet AC = CB car le triangle ACB qui a une hauteur médiane est isocèle.
Et comme BC = BD par construction, on a : AC = BC = BD.
Après la rotation du triangle, on retrouve les égalités :
AG = EG = EF = AC = BC = BD
Le triangle GKF est rectangle et KE est médiane relative à l'hypoténuse, donc KE = EF = EG
(c'est le rayon du cercle circonscrit au triangle rectangle)
Finalement on retient les égalités : KE = EG = AG = AC
Appelons K, E, G, A et C les angles du pentagone,
les autres seront nommés avec 3 lettres.
Le triangle KEG est isocèle.
Traçons sa médiatrice (EH) .
On a dans le triangle KEH :
(K -90°) + E/2 + 90° = 180°
donc K + E/2 = 180°
finalement on a dans le pentagone 2K + E = 360°L'angle DCK est de même mesure que l'angle C (symétrie / à (OC).
et l'angle G est de même mesure que ACD
(rotation de construction).
On a 2C +ACD = 360°
Donc dans le pentagone 2C + G = 360°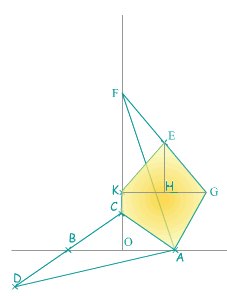
(1) DAVID WELLS Dictionnaire Penguin des curiosités géométriques éditions Eyrolles
