La
saga des pavages pentagonaux
construits avec des pentagones IRREGULIERS
15 types de pavages
construits avec des tuiles pentagonales irrégulières sont
actuellement découverts.
Il n'est pas aisé de paver le plan avec des pentagones. On
sait que c'est impossible avec des pentagones réguliers.
Cependant nous connaissions déjà 14 modèles de
pentagones particuliers pavant le plan.
Le 16 août 2015, trois mathématiciens (Casey Mann, Jennifer
McLoud and David Von Derau) de l’Université de Washington
Bothell, ont découvert une nouvelle façon de paver le
plan en utilisant exclusivement des pentagones.
Sous la direction des deux premiers, le troisième, a écrit
un programme qui a découvert un quinzième pavage du
plan :
expérimentation et animation pas à pas ICI.
Les
15 pavages pentagonaux interactifs, avec des tuiles irrégulières
modifiables
Cliquer le pavage
désiré.
Chaque pavage est animé pas à pas.
Le mode AUTO permet de voir défiler la construction du pavage
de façon automatique.
Dans le mode MANUEL on avance pas à pas.
Les boutons couleur donnent un coloriage organisé de toutes
tuiles
Cependant, chaque tuile peut être coloriée indépendamment
des autres en utilisant le bouton couleur en haut à
droite :
Choisir avec ce bouton la couleur désirée et cliquer
ensuite la ou les tuile(s) à modifier.
Quand les sommets du pentagone de base sont visibles (ils
ne le sont pas lors des translations mais réapparaissent à
la fin de chaque translation),
on peut déformer le pentagone de base. Il gardera les propriétés
liées au type de pavage en construction.
Quand la construction est complète, l' EMPREINTE du pavage
est visible et
on peut recommencer en cliquant le bouton fléché à
droite en mode AUTO ou MANUEL.
CLIQUER
chaque image
Pavage
de type 1

Deux angles supplémentaires
et deux côtés parallèles :
D + E = 180° donc CD // AE.
 |
Pavage
de type 2

Deux angles supplémentaires
et deux côtés égaux :
C + E = 180° ET AE = DC.

|
Pavage
de type 3

Trois angles de 120° et deux
côtés égaux. :
AB=AE et BC+ED=CD.
 |
Pavage
de type 4
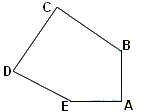
Deux angles droits et
deux couples de côtés égaux :
A = 90° et C
= 90°
EA = AB et DC = CB.
 |
Pavage
de type 5
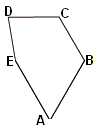
Deux angles supplémentaires
et deux côtés parallèles :
A = 60° ; C = 120°
EA = AB CD = CB.
 |
Pavage
de type 6
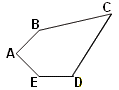
Deux angles
supplémentaires C et E
puis A = 2C
EA = AB = DE et BC = CD.
 |
Pavage
de type 7

C + 2B = 2π
et A + 2D = 2π
puis
EA = AB = BC = CD.
 |
Pavage
de type 8
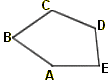
2D + C = 2π
et B + 2A = 2π
puis
EA = AB = BC = CD.
 |
Pavage
de type 9
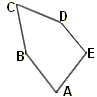
B + 2E= 2π
et C + 2D = 2π
puis
EA = AB = BC = CD.
 |
Pavage
de type 10
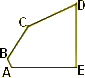
A + D = π ; E = π / 2
et 2C + D = 2π
puis
EA = ED et AB + CD = AE.
 |
Pavage
de type 11

C + E = π ; A = π / 2
et 2B + C = 2π
puis
ED = DC et DE = 2 EA + CB.
 |
Pavage
de type12
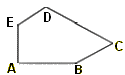
C + E = π ; A = π / 2
et 2B + C = 2π
puis
CD = 2EA et 2EA = CB + DE.
 |
Pavage
de type 13
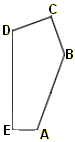
E = C = π/2 ;
2D = 2A = 2π - B
puis
CD = CB et DE = 2 CD.
 |
Pavage
de type 14
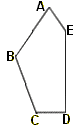
D = π/2 ;
2E + A = 2π, C + A = π
puis
CD = AE et AB = BC = 2CD.
 |
Pavage
de type 15
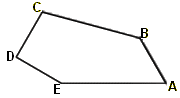
A =60°, B = 135° ,
C = 105°,
D= 90° et E = 150°.
AB = CD = DE = EA/2
CB = AB 
 |
Un
petit effet ressort peut apparaître lors d'un déplacement
très rapide des points sur certains pavages
dont les rotations dépendent de l'angle du motif de base (par
exemple le pavage de type 6, 12 ou de type 13).
C'est normal, tout se met parfaitement en place lorsqu'on relâche
la souris.
Voir
aussi
le travail de Pierre Crespin sur les pavages ICI :
http://picresp.free.fr/eNETetMATHS/CabriJava/Penta%2015/index%20Penta15.html
OU
http://picresp.free.fr/eNETetMATHS/





























