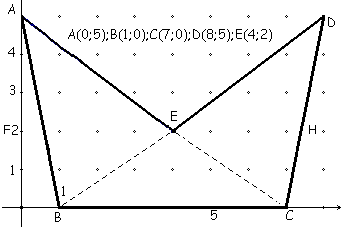
Le bonnet d'âne . Le bonnet Solution   Le bonnet Prof, pose un problème dans sa classe :        Il s'agit de calculer l'aire du bonnet d'âne ci-dessous avec les coordonnées des points A,B,C,D,E notées sur la figure.        Très simple quand on sait calculer l'aire d'un trapèze ou d'un triangle !        Chacun y va de sa méthode et finalement nous obtenons les résultats suivants :   Première méthode : calcul de la différence des aires du trapèze (ABCD) et du triangle (AED).         Aire (ABCD) - Aire(AED) =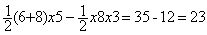 Deuxième méthode : calcul direct .         Aire (ABC) + Aire(BDC) - Aire(BEC) = Chacune des deux méthodes semble exacte, pourtant les résultats sont différents. Y-a-t-il un bon résultat ? Si oui quel est le bon ? Et où est l'erreur ?   Solution  Les deux procédures semblent exactes a priori. Mais la deuxième procédure utilise l'alignement des points A, E et C, tout comme celui symétrique des points D, E et B. Or ces points ne sont pas alignés. En effet, s'ils l'étaient, nous aurions égalité pour la tangente des angles AEF et HEC.        Or tangente(AEF) = 3/4        et tangente(HEC) = 2/3        et 3/4 2/3. On peut vérifier que la droite (AC) ne passe pas par E, en posant la souris sur la figure ci-dessous. Par le calcul on vérifie bien que le point d'intersection des deux droites (AC) et (BD) n'est pas E : (AC) d'équation y = -(5/7) x + 5 et (BD) d'équation y = (5/7) x + - 5/7 ont pour intersection le point d'abscisse x =4 et d'ordonnée y =15/7.   Donc le résultat exact est le premier qui utilise la différence d'aire du trapèze et celle du triangle sans faire intervenir les droites (AC) et (BD) : c'est 23. On peut retrouver ce résultat avec la formule de Pick en comptant les points du réseau qui sont sur le tour de la figure : 10 puis ceux qui sont à l'intérieur : 19. La formule donne l'aire : 10/2 + 19 - 1 = 23. .