Comptons les points Comptons les côtés des carrés Comptons les mailles Ou comment déterminer l'aire d'un polygone simple en comptant seulement soit des points, soit des côtés soit des mailles.

 

Comptons les points

Compliquée la forme de votre figure ? Pourtant en prenant comme unité un carreau du  réseau dessiné,  
nous calculerons très simplement son aire, c'est à dire la mesure de  sa surface.
Nous allons tout bonnement compter des points !

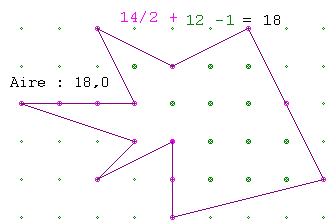
Déplacer ci-dessous les points numérotés de 0 à 9 sur le réseau.
On peut utiliser la souris ou bien les quatre flèches du clavier.

Surtout ne pas croiser les côtés et respecter l'ordre des sommets.

CLIQUER

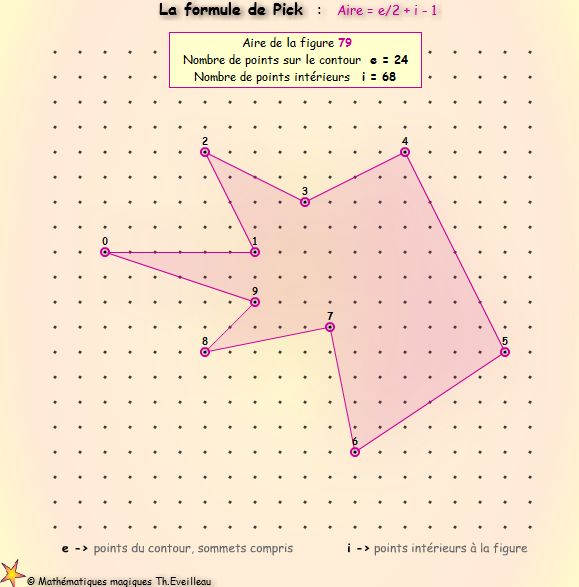
Soit e le nombre de points du réseau qui touchent les côtés, sommets compris (14 ci-dessous).
Soit i le nombre de points qui sont à l'intérieur de la figure (12 ci-dessous). 

Georg Alexander Pick (autrichien né à Vienne le 10 août 1859 , décédé en 1942) présenta son théorème en 1899.

Il étudie les mathématiques et la physique à l'université de Vienne de 1875 à 1879 et obtient, en 1880, le grade de Docteur de l'université de Vienne.
En 1888, il est Professeur de mathématiques à l'université allemande de Prague.
Il était juif et bien qu'ayant fui à Prague en 1938, il fut déporté dans le camp de concentration de Theresienstadt en 1942, où il mourut le 26 juillet de cette même année.
Georg Alexander PICK a contribué de manière significative à l'analyse et à la géométrie différentielle en publiant près de 70 articles.
Il présenta à Albert Einstein les travaux de grands mathématiciens qui aidèrent ce dernier à développer sa théorie générale de la relativité.

Les mathématiciens ont découvert depuis, qu'il n'existe pas de théorème, directement équivalent en trois dimensions, qui permette de calculer le volume d'un polytope en comptant les points internes et les points du bord.

En savoir plus et démonstration ici :
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Pick

Dans le commerce sont ven

dues des planches à clous
appelées aussi géoplans