Pour la troisième
aiguille des secondes, il faut d'abord que les deux premières
se superposent : alors on regarde uniquement les onze résultats
calculés ci-dessus et... on ne trouve aucun cas où la
troisième se superpose à la seconde près sauf
à midi ou à minuit : il faut pour cela que le nombre
de secondes soit identique à celui des minutes...
Par contre si l'on est moins exigeant, à 5 secondes près
par exemple nous avons une superposition à 3 heures 16 minutes
21 secondes.
Le graphique
suivant (proposé par Pierre Jullien) permet de voir le
problème sous un autre angle :
les traits obliques fins représentent le parcours de la grande
aiguille et le trait plus épais représente celui de
la petite aiguille.
L'axe horizontal représente le temps qui s'écoule en
heures et l'axe vertical reflète les positions des aiguilles
sur le bord déroulé du cadran horaire.
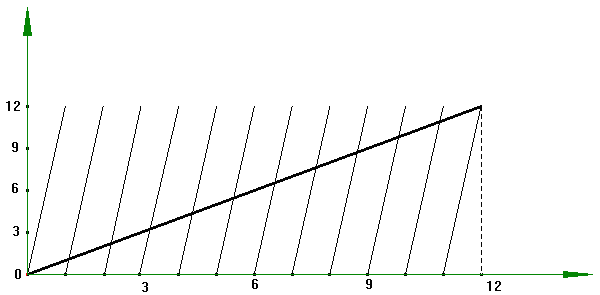
Nous
retrouvons les solutions aux intersections des traits. Cela donne
11 solutions en comptant le départ : 12h 0 minute 0 seconde
ou 0 heure 0 minute 0 seconde.
Paradoxe des
aiguilles
1 heure
c'est 60 minutes, pourtant l'aiguille des minutes ne va que 12 fois
plus vite que celle des heures !
1 minute c'est
60 secondes et l'aiguille des secondes va bien 60 fois plus vite que
celle des minutes ;o)
La petite blague de Christophe
Un esquimau se trouvant sur la banquise attend impatiemment sa douce
moitié qui est en retard pour un rendez-vous galant.
Il sort alors un thermomètre de sa poche et se dit :"Si
elle n'est pas là à moins 20, je m'en vais ! "