Russell et le Pape

Un étudiant en philosophie demanda à Russell quelques éclaircissements :
"Prétendez-vous que de "2+2 = 5", il s'ensuit que vous êtes le Pape ? "
"Oui", fit Russell.
L'étudiant étant sceptique Russell proposa la démonstration suivante :
        (1) Supposons que 2 + 2 = 5.
        (2) Soustrayons 2 de chaque membre de l'identité, nous obtenons 2 = 3.
        (3) Par symétrie, 3 = 2.
        (4) Soustrayons 1 de chaque côté, il vient 2 = 1.       

Maintenant le Pape et moi sommes deux. Puisque 2 = 1, le Pape et moi sommes un. Par suite je suis le Pape.

 

 

 

Avec des si ...

"Avec des si... on referait le monde" ...
"Si les poules avaient des dents alors j'irai sur la lune... " sont des expressions populaires.
"Si 2+2=5, alors je suis le Pape" démontrait Russell.

Ces trois phrases ont en commun le principe de logique qui affirme que :

Toute proposition peut être déduite d'une proposition fausse.
Il faut bien l'avouer nous sommes un peu choqués dans un premier temps.

 

L'implication logique

Derrière cette forme très peu intuitive se cache l'implication logique.
Trois propositions sont ici en jeu :
        . la prémisse P dans l'implication P => Q
        . la fin Q : la conclusion
        . la phrase entière qui correspond à l'implication complète.      

Mathématiquement, il sagit de l'implication logique.
Elle étudie aussi le cas où la prémisse est fausse.
Dans la vie courante nous ne considérons que très peu ce cas qui nous choque, nous considérons P comme vraie.

On établit la table de vérité de l'implication ainsi :

L'expression (A implique B) est vraie quand
        .A vrai et B vrai          assez intuitif
        .A faux et B faux        peu intuitif
        .A faux et B vrai         pas intuitif (c'est ce cas qui est utilisé dans les phrases ci-dessus).

L'expression (A implique B) est fausse quand
        .A vrai et B faux          intuitif .

L'implication logique n'est fausse que dans le cas où la prémisse P étant vraie Q est fausse.
C'est lorque A est faux seulement que cette définition n'est plus intuitive. 

Le jeu mathématique

Nous sommes ici dans le jeu des mathématiques ; celui qui a pour règle leprincipe du "tiers exclus" .
    Pour un énoncé A bien formulé, il n'y a que deux possibilités :
    ou bien A est vrai ou bien c'est le contraire de A qui est vrai.
On a donc posé des règles logiques très strictes assurées de ne jamais déboucher sur deux conséquences contradictoires l'une de l'autre.
Ces définitions prennent souvent du sens dans des situations de la vie pratique ou sociale. Mais ce n'est pas toujours le cas et on a quelquefois des paradoxes apparents (notamment lorsqu'on touche à l'infini) comme :
"La partie peut être aussi grande que le tout"
"la moitié de quelquechose peut être égale en nombre à cette chose tout entière."
"Il y a autant de nombres pairs que d'entiers."

Alors Cantor se posait une autre question :
"Puis-je parler del'infini sans rencontrer de contradictions ?"

 

 

 

 Amusements logiques

 

 

Solutions

...

Oui trois propositions sont fausses, les voici :         2 = 1         18 / 3 = 4 et ;-)         trois sont fausses : Mais alors la dernière devient vraie, donc il n'y a plus que deux propositions fausses. Nous nous retrouvons en pleine contradiction comme dans le barbier (2). Le problème vient du fait que la proposition trois sont fausses est incluse à la fois dans la question et les propositions... Kurt Gödel a démontré qu'à ce niveau on est toujours bloqué.

Mazda n'est ni au milieu ni à gauche, donc il est à droite.
        Comme Mazda dit la vérité, Lucifer est au milieu.
        Enfin Masoud est à gauche.

 

Le crocodile dévorera sans doute le petit ;o)

Si le crocodile dévore le petit, alors la mère a raison et le crocodile doit le lui redonner.
MAIS Si le crocodile ne dévore pas le bébé, alors la mère s'est trompée et le crocodile doit donc le dévorer !
La situation est contradictoire, on tourne en rond ...

Aussi Lewis Carroll propose la solution suivante pleine de bon sens :
Si le crocodile dévore le petit, la mère a raison et le crocodile est de mauvaise foi.
Si le crocodile ne dévore pas le petit, la mère a tort et le crocodile est encore de mauvaise foi.
De toute façon, le crocodile manquera à sa parole. On ne peut pas lui faire confiance !
Il mangera sans aucun doute le bébé, c'est sa nature ;-)

L'interne de service est la maman ! (Paternité et Maternité se conjuguent non ? ;-)

NON ! ! ! pas Poum mais TOTO ;o) c'est un classique... 

La bonne blague, craquez l'allumette... ;o)

 

Russell, Gödel...

Bertrand Russell, mathématicien logicien philosophe britannique 1872-1970.

La rencontre de Russell avec son professeur Whitehead amène les deux hommes à réfléchir sur le fondement des mathématiques. Ils développent ce que l'on appelle le logicisme. Les deux hommes définissent des propositions qui prennent la valeur vraie ou fausse , et des fonctions propositionnelles qui sont des propositions dépendant d'une variable. Ils définissent les connecteurs et leur valeur de vérité en fonction de celles des propositions qui leurs sont appliquées. Ils donnent des postulats non démontrables. Il en découle les théorèmes de la logique.

Russell et Whitehead se rendent compte qu'un paradoxe peut apparaître, en théorie des ensembles, lorsqu'une collection d'objets en contient un qui est défini par la collection elle-même. Ils bâtissent alors la théorie des types pour tenter d'éviter ces paradoxes.
Le plus gros reproche fait à cette théorie est que dans ce système, toutes les mathématiques se déduisent de manière purement formelle, et donc toute intuition ou apport de l'expérience sensible en est exclue.

Paradoxe de Russell (familiarisé par celui du barbier en 1918)

Considérons l'ensemble A ={X 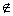/ X X}.
On doit avoir A A ou A 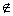A, mais chacune de ces hypothèses conduit à une contradiction.

Petite anecdote

L'été 1919, Littlewood enthousiasmé expliqua à Russell la théorie d'Einstein sur la relativité, Russell qui à cette époque ne connaissait rien à la physique explosa : "Dire que j'ai passé toute ma vie dans la boue de l'ABSOLU."

 

 

Kurt Gödel, logicien américain (1906-1978) d'origine autrichienne.

Les travaux de Gödel touchent uniquement la logique mathématique. Leur célébrité provient du fait qu'ils démentent les conceptions que l'on a jusque-là des fondements des mathématiques et qu'ils posent de nouveaux problèmes philosophiques. Hilbert et Ackermann posent en 1928 la question : Etant donné un système formel avec un langage, des axiomes et des règles de déduction et une notion d'interprétation dans des structures mathématiques, toute assertion vérifiée dans toute interprétation est-elle formellement déductible des axiomes ?

Gödel répond en 1929 par l'affirmative.I
Il démontre le théorème de complétude du calcul des prédicats. Puis il démontre en 1930 et 1931 ses deux théorèmes d'incomplétude ; Ces théorèmes prouvent que toute théorie mathématique dans laquelle on peut formaliser l'arithmétique ne peut prouver en elle-même sa non-contradiction. (1)

Petite anecdote

.Quand Gödel arriva en Amérique, il subit un petit examen pour sa naturalisation.
En étudiant la constitution des Etats-Unis, il décela de nombreuses contradictions logiques et remarqua que rien n'empêchait en toute légalité, l'avènement d'une dictature.
Il fit part de ses découvertes à son ami Oscar Morgenstern qui lui conseilla de ne rien en dire à son examen de citoyenneté. 
.Toute sa vie Gödel souffrit de dépression nerveuse et d'hypocondrie. On dit aussi qu'il avait peur d'avoir peur d'être malade (sorte de récurrence qui rejoindrait d'une certaine manière ses travaux... ). Il se laissa mourir de faim le 14 janvier 1978.

 

Syllogismes

On construit un raisonnement logique avec des syllogismes. Le plus connu de l'histoire fut énoncé par Socrate (Athènes, 470-399 avant J.-C.) :
       Tous les hommes sont mortels,
        Or je suis un homme,
        Donc je suis mortel.
Un syllogisme est cmposé de trois phrases :
les deux premières énoncent une relation entre trois choses (ici : les hommes, les mortels et je : Socrate)
et la troisième est une conséquence logique des deux premières.

Aristote (Stagire, 384-322 avant J.-C.) étudia toutes les catégories de syllogismes. Beaucoup de logiciens les ont travaillé. Voici quatre extraits de Logique sans Peine (éd Hermann, 1966).
Pour chacun de ces syllogismes indiquez si la conclusion est
certainement exacte,
certainement fausse,
ni certainement exacte, ni certainement inexacte.

     

Quelques cravates sont de mauvais goût. J'admire tout ce qui est de bon goût. Il y a quelques cravates que je n'admire pas.	Aucun singe n'est soldat. Tous les singes sont malicieux. Quelques créatures malicieuses ne sont pas des soldats.
Aucun fossile ne peut être malheureux en amour. Une huître peut être malheureuse en amour Les huîtres ne sont pas des fossiles.	Aucun empereur n'est dentiste. Tous les dentistes sont redoutés par les enfants. Aucun empereur n'est redouté par les enfants.

Solutions

Ni certainement exacte, ni certainement inexacte. On ne sait pas.	Exacte.
Exacte.	Ni certainement exacte, ni certainement inexacte. On ne sait pas.

 

 

(1) Source : B.Hauchecorne et D.Surreau Des mathématiciens de A à Z éditions ellipses

(2)Au début du XXème siècle, Bertrand Russell et plus tard Rudolf Carnap (Théorie dite des types logiques), montrent que les entités logiques ne sont pas toutes de même type. Le "tout" dans un ensemble d'objets n'est pas du même type que les objets eux-mêmes