La rotondité de la Terre se projette sous nos yeux lors d'une éclipse de lune. Elle s'est imposée au IVème siècle avant notre ère entre Platon et Aristote.
Strabon (v. 58 av. J.-C.- 23 apr. J.-C.) donne un indice supplémentaire : lorsqu'un bateau s'éloigne d'un port, sa coque, progressivement masquée par l'horizon (la courbure de la Terre), disparaît avant son mât.

Cliquer cette l'image pour voir l'animation qui permet de calculer les distances à l'horizon.   Voir les différentes planètes ICI avec un mnémo pour mémoriser l'ordre des planètes.

Source et illustration : Almanach Hachette 1924

Eratosthène allait un peu plus tard donner une mesure de la circonférence du globe.

Eratosthène, géographe et mathématicien (*1) Eratosthène (Cyrène environ 276 av.J.-C - Alexandrie, environ 194 av.J.-C) était astronome, géographe, philosophe et mathématicien grec du IIIe siècle avant notre ère (né à Cyrène, aujourd'hui Chahat en Libye, v. -276 ; mort à Alexandrie, Égypte, v. -194). Il fut l'élève d'Ariston de Chios.Il a été directeur de la bibliothèque d'Alexandrie. Il est célèbre pour être le premier dont la méthode de mesure de la circonférence de la Terre soit connue. On a donné son nom à l'astéroïde (3251) Ératosthène5, ainsi qu'au cratère lunaire Eratosthène. Il avait entendu des voyageurs raconter qu'à Syène (Assouan), le 21 juin à midi, on pouvait voir l'image du Soleil se refléter au fond d'un puits. Cela signifiait évidemment que le Soleil était alors exactement à la verticale du puits. Son expérience Le 21 juin, à midi, à Alexandrie, Eratosthène mesure la longueur de l'ombre d'un obélisque de la ville. Par un calcul de géométrie simple, il montre alors que le Soleil fait un angle de 7°12' avec la verticale (mesure très proche de la réalité parce que la vraie mesure est d'environ 7°8' ) (*2). 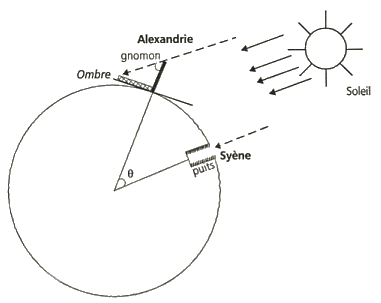Les angles marqués ci-dessous sont égaux comme angles alternes-internes. La distance entre les parallèles séparant les villes est proportionnelle à la mesure de l'angle dont le sommet est au centre de la Terre. Les bématistes ont trouvé que la distance Syène-Alexandrie était de 5000 stades de 157,5 m donc d'environ 787,5 km. Eratosthène trouve alors la longueur de la circonférence de la Terre : 39375 km ce qui est très proche de la réalité. Faire un petit calcul de proportionnalité :                                 7°12' donnent 787,5 km, et                                 360° donnent (787,5 x 360) / 7,2 km.                                          N'oublions pas que                                 12 minutes correspondent à 0,2 degré car                                60 minutes correspondent à 1 degré On peut aussi noter que 7°12' représentent 1/50 ème du tour de la terre. Remarque La différence de longitude entre Syène et Alexandrie introduit une erreur non négligeable. Cela peut intervenir sur le résultat d'Eratosthène, elle a peut-être compensé l'erreur de mesure de la distance entre Syène et Alexandrie calculée à partir de journées de marche. Eratosthène avait sans doute conscience d'avoir trouvé une approximation de la circonférence de la Terre sans peut-être...(?) en maîtriser la précision.

Notons que la longitude d'Alexandrie est d'environ 30° et la latitude de 31°.
Pour Syène (Assouan) la longitude est d'environ 32° et la latitude de 24° 05’.

Voici comment Denis Guedj rapporte, dans" les cheveux de Bérénice" (2003), la première lettre d'Eratosthène parti mesurer la distance Alexandrie-Syène, à Philopator roi d'Egypte :
"Afin d'assurer la justesse des résultats, il est capital que je dispose d'un double comptage. Voici la solution à laquelle je me suis arrêté.
Béton marchera le long de la berge, comptant mentalement le nombre de pas accomplis. Derrière lui, à petite distance, Théophraste Excelsior pratiquera en silence, un second comptage. J'insiste sur l'importance de l'indépendance de ces deux comptages. Pour s'en assurer, j'ai demandé à Béton et à Théo, dès leur arrivée, de noter chacun de leur côté le nombre de pas comptés. Si l'écart est faible, je retiendrai la moyenne des deux nombres. Dans le cas contraire, nous serons contraints de recommencer depuis la précédente halte...
Un problème subsiste : comment le deuxième compteur, qui n'est pas bématiste, pourra-t-il suivre le rythme ? S'il se déplaçait à pied, il serait vite devancé. J'ai donc imaginé une solution qui me semble offrir bien des avantages. Théophraste Excelsior se déplacera sur un âne trottant derrière Béton. "

A vous

Vous pouvez tenter l'expérience avec un ami, c'est facile avec le téléphone. Nul n'est besoin d'avoir le soleil au zénith. Choisissez deux villes assez lointaines sur le même méridien, et s'il y a du soleil dans les deux villes tentez l'expérience :
dans chaque ville, choisir un monument ou un arbre dont vous connaissez la hauteur (Cf mesurer la hauteur d'un arbre) et mesurez la longueur de l'ombre.
Calculez le rapport
                                k = (longueur ombre) / (hauteur arbre).
Avec une calculette et la fonction arctangente, déterminer l'angle que fait le soleil avec la verticale :
                                angle = arctangente(k)
Si les villes sont dans le même hémisphère calculez la différence des deux valeurs trouvées, sinon ajoutez les, comme ci-dessous.
Vous pouvez alors lire sur le schéma interactif ci-dessous la distance des parallèles séparant les deux villes, ou bien retenter le calcul de la circonférence de la terre, si vous connaissez la distance entre les parallèles séparant les deux villes. 

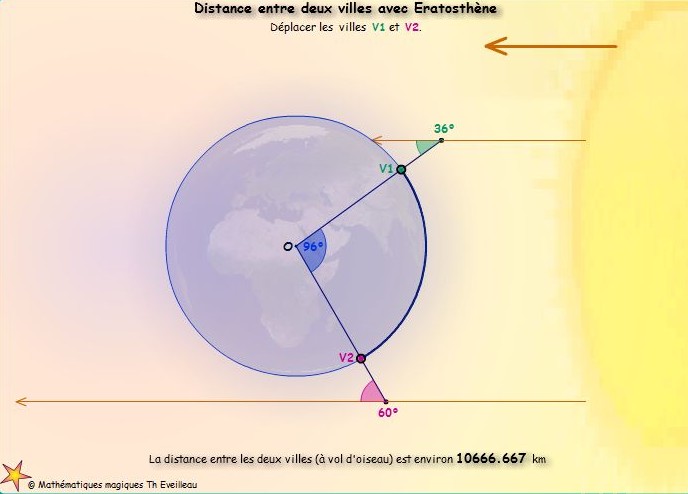
Dans l'animation suivante déplacer avec la SOURIS ou le CLAVIER (avec les quatre flèches) les villes V1 et V2.

La distance aérienne est alors automatiquement affichée.

Petite explication

Villes dans deux hémisphères différents

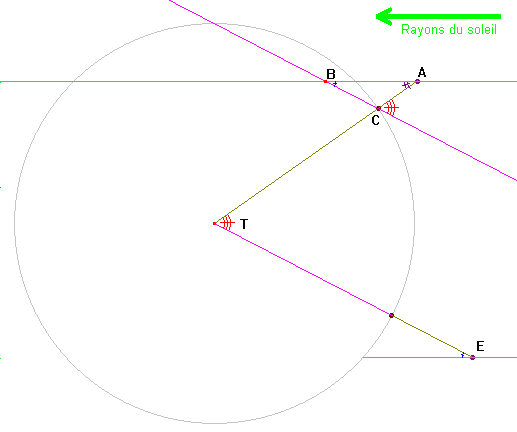
En utilisant l'égalité des angles correspondants ou ayant leurs côtés parallèles, et la somme des angles du triangle ABC, nous vérifions que l'angle au centre de la terre est la somme des angles obtenus dans les deux villes : Â + Ê.

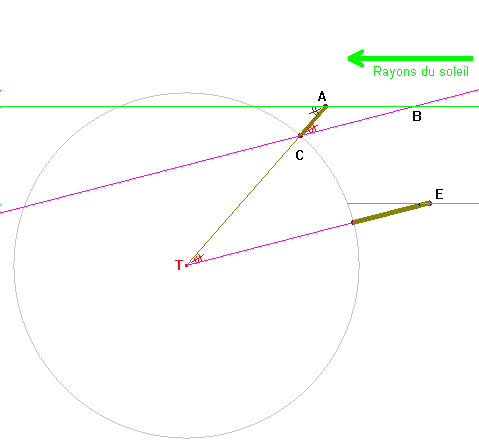
Villes dans le même hémisphère
Cette fois, nous vérifions que l'angle au centre de la terre est la différence des angles obtenus dans les deux villes : Â - Ê.

Voir aussi un document d'après un ouvrage de géographie 1868
http://pagesperso-orange.fr/bernard.langellier/systeme-solaire/eclipses-terre-ronde.htm

 

Les débuts de la géométrie en Grèce de Michel Serres ^(*1)
"Voici comment calcule Ératosthène (276-195 av. J.-C.). Il pose un gnomon à Syène en Égypte non loin de la première cataracte du Nil, ville située sur le tropique du Cancer. En ce lieu, il ne fait pas d'ombre à midi le jour du solstice d'été. Le même jour à la même heure, Ératosthène mesure l'angle que fait le Soleil avec un second gnomon posé dans la ville d'Alexandrie qu'il pensait située sur le même méridien. L'angle qu'il a mesuré vaut la cinquantième partie d'un cercle, il suffit donc de multiplier par cinquante la distance d'Alexandrie à Syène pour obtenir la longueur entière du méridien terrestre. Résultat grandiose obtenu avec des moyens minimaux. Pour améliorer la mesure, Ératosthène estime l'ombre du gnomon non point projetée sur un plan, mais sur une sphère ou peut-être le polos dont parle Hérodote dans le lieu déjà cité."

Civilisation grecque André Bonnard d'Euripide à Alexandre de André Bonnard éditions complexe 1991

Pour cela on calcule la tangente de l'angle qui est égale au rapport de la longueur de l'ombre par la hauteur de l'obélisque ^(*2)