L'anse de panier

L'anse dynamique à trois cercles Le programme de construction Pourquoi cela marche : démonstration L'anse à cinq cercles : construction
Ce n'est pas facile D'avoir ton équilibre, Avec cette pression En chacun de tes points ...		D'un extérieur uniforme... Tiraillée que tu es Sur ton parcours entier... Guillevic 1967

L'anse à trois cercles

Il y a quelque temps, un maçon de mes amis m'a demandé la construction d'une anse de panier.
Il ne parlait pas de l'anse du panier dans lequel je ramasse les champignons en automne.
Son projet était de réaliser une belle entrée dans un manoir.

L'anse de panier est une approximation d'une demi-ellipse par un nombre impair de cercles.
Pour avoir une belle courbe, ces cercles doivent avoir la même tangente au point de raccordement.

Nous allons étudier une approximation obtenue par un ensemble de trois cercles.

Pour en savoir plus sur différentes constructions d'une l'ellipse voir Ellipse dans trucs maths (rubrique courbes).
La construction proposée est très simple. Elle est harmonieuse et permet de choisir la hauteur de la voûte.
Noter la véritable ellipse rigoureuse tracée discrètement en jaune.
On remarquera que la différence n'est visible que pour de petites valeurs de OC.


Dans l'animation ci-dessous, on peut déplacer les points C et A avec la SOURIS ou bien avec les flèches du CLAVIER.
-le point A modifie la largeur de l'anse ;
-le point C modifie la hauteur de l'anse.

 

CLIQUER

     

  Construction

- Construire le cercle (C) de centre O et de rayon [OA].
- Construire le rayon [OH] perpendiculaire en O à [OA].
- Choisir un point C sur [OH], selon la hauteur OC désirée pour l'anse.
- Tracer le segment [CA].
- Tracer le cercle (C') de centre C et de rayon [CH].
- Ce cercle (C') coupe le segment [AC] en K.
- Tracer la médiatrice (D) de [AK] (droite perpendiculaire à [AK] en son milieu I).
- Cette médiatrice (D) coupe la droite (OH) en O2 et la droite (OA) en O1.
- Tracer le cercle de centre O1 et de rayon O1A ; cet arc coupe la médiatrice (D) en B.
  Ne garder que le petit arc de cercle allant de A vers B.
- Tracer le cercle de centre O2 et de rayon O2C.
  Ce cercle passe par B (nous allons le démontrer ci-après), ne garder que le petit arc allant de B vers C.
- Compléter les deux arcs par symétrie par rapport à l'axe (OC).
Nous obtenons ainsi l'anse de panier colorée en rose et vert.    

CLIQUER

   

Démonstration

 

 

Soit I le milieu de [AK].
Les égalités des mesures d'angles, notées sur la figure, se justifient parce que
les angles ont leurs côtés respectivement perpendiculaires deux à deux.
Posons a = OA ; b = OC ; c = AC. Alors CH = a - b.
Des triangles ayant des angles respectivement de même mesure sont semblables.
Ainsi le triangle O1 I A est semblable au triangle COA donc 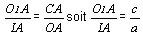(Equation G).
Le triangle O1OO2 est semblable au triangle COA donc 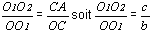(Equation E).
De même nous obtenons :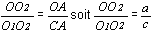 (Equation F).

Cherchons la longueur O2B O2B = O1A + O1O2 Nous avons avec l'équation G, . Et   OO1 = a - O1A   donc Avec l'équation E, nous obtenons : Comme O2B = O1A + O1O2, il vient Nous savons que  c² = a² + b².

Finalement Cherchons la longueur O2C Avec l'équation F, on a :

Nous venons de démontrer que O2B = O2C.
Cela montre que l'on peut construire le cercle de centre O2 passant par C et B.
La construction est licite et les deux cercles utilisés pour construire l'anse ont une tangente commune en le point B,
puisque les supports des rayons sont identiques et que la tangente en un point d'un cercle est perpendiculaire au rayon qui aboutit à ce point.

En tapant anse panier dans votre moteur de recherche préféré, vous trouverez d'autres constructions plus ou moins compliquées avec plusieurs arcs.
Ci-après je vous en propose une, magnifique, construite à partir de cinq cercles.
Il semble qu'elle ait été utilisée pour la construction de certaines voûtes du XI^e et XII^e siècles.

L'anse à cinq cercles

Voici le programme de construction de l'anse à cinq cercles.

- Tracer la droite de base, sur laquelle on place le point U.
- Reporter cinq segments de même longueur UA.
- Tracer la médiatrice du segment [UV].
- Construire les points J et C sur cette médiatrice, tels que OJ = UA et JC = UA.
- Tracer la demi-droite [JA).
- Le cercle de centre A passant par U, coupe [JA) en les points K et B.
- On obtient l'arc UK.
- Tracer la demi-droite [CB).
- Le cercle de centre B passant par K coupe [CB) en le point L.
  Ne garder que l'arc de cercle KL.
- Le cercle de centre C passant par L coupe la médiatrice en le point L.
  Ne garder que l'arc de cercle LM.
- Compléter la figure avec la symétrie axiale par rapport à la médiatrice (CM).
On obtient une anse de panier à cinq cercles.

 

CLIQUER