Avec
deux cercles
Traçons
deux cercles concentriques après avoir choisi leurs rayons
respectifs.
Choisissons également le nombre d'étapes du tracé.
Les diamètres des deux cercles seront les axes de l'ellipse.
Traçons un certain nombre de rayons et continuons la construction
en suivant l'animation ci-dessous..
Nous obtenons une belle ellipse.
Ce procédé était, semble-t-il, enseigné
à l'école pratique (ancêtre des LEP) en 1940.
CLIQUER

Quelques
explications
Choisissons le
repère formé du centre de l'ellipse et des deux axes
horizontaux et verticaux de l'ellipse.
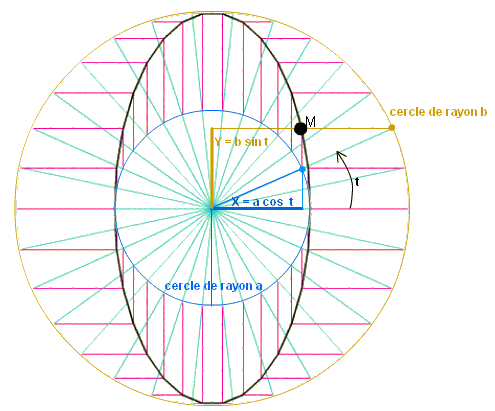
Appelons a et b les rayons des deux cercles initiaux.
Si
nous appelons t, l'angle du rayon vert avec l'horizontale, le point
M intersection des deux segments rouges a pour coordonnées
X = a cos t et Y = b sin t.
Il s'agit de l'équation paramétrée de l'ellipse.
Ces relations permettent de retrouver l'équation cartésienne
:
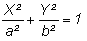
Nous pouvons aussi définir l'ellipse à partir de ses
foyers A et B.
M étant un point de l'ellipse, la longueur de la corde ABMA
est constante.
Nous retrouvons ci-dessous, la méthode des jardiniers pour
tracer cette courbe.

Avec
une corde de longueur constante : la corde du jardinier
Dans l'animation ci-dessous
On déplace le point M en
tirant sur la corde dont la longueur reste constante.
Cette corde est fixée sur les deux points fixes
F et F' qui
sont les foyers de l'ellipse.
Avec OA = a OB =b.
Si a> b, le
petit axe de l'ellipse est de longueur 2b
et le grand axe est de longueur 2a.
Si a>b c'est linverse.
Si a=b, nous avons un cercle.
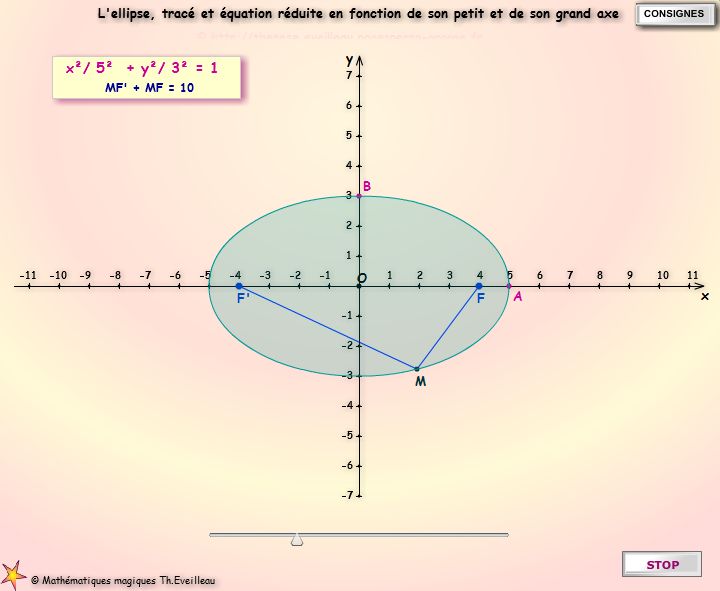
L'équation
réduite de l'ellipse dans le repère orthogonal centré
en O est :
x²/a² + y²/b² = 1
Les boutons STOP et ANIMER arrêtent
ou relancent le déplacement du point M.
On
peut déplacer MANUELLEMENT les points M
(SOURIS),
A
et B
(SOURIS ou
CLAVIER) après avoir
cliqué le bouton STOP.
Avec la SOURIS
Déplacer le point A pour
modifier le grand axe de l'ellipse et B
pour modifier le petit axe de l'ellipse.
Déplacer le point M avec
la SOURIS et
noter que MF'+ MF
=2 a, est constant pour chaque ellipse : MF'
+ MF = 2 * OA.
Grâce à cette propriété on peut tracer
comme le faisaient les égyptiens une ellipse avec la
corde du jardinier, cF ICI.
Au CLAVIER
-les flèches HAUT et BAS
modifient le point B
;
-les flèches GAUCHE et DROITE
modifient le point A.
CLIQUER

Une
jolie application
avec le théorème de Pythagore


