Avec
deux cercles
Traçons
deux cercles concentriques après avoir choisi leurs rayons
respectifs.
Choisissons également le nombre d'étapes du tracé.
Les diamètres des deux cercles seront les axes de l'ellipse.
Traçons un certain nombre de rayons et continuons la construction
en suivant l'animation ci-dessous..
Nous obtenons une belle ellipse.
Ce procédé était, semble-t-il, enseigné
à l'école pratique (ancêtre des LEP) en 1940.
 PLEIN
ECRAN
PLEIN
ECRAN
Quelques
explications
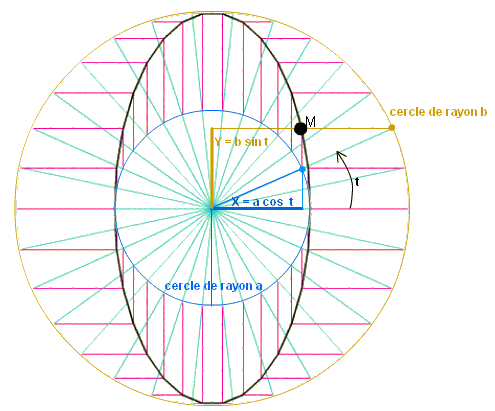
Choisissons
le repère formé du centre de l'ellipse et des deux
axes horizontaux et verticaux de l'ellipse.
Appelons a et b les rayons des deux cercles initiaux.
Si
nous appelons t, l'angle du rayon vert avec l'horizontale, le point
M intersection des deux segments rouges a pour coordonnées
X = a cos t et Y = b sin t.
Il s'agit de l'équation paramétrée de l'ellipse.
Ces relations permettent de retrouver l'équation cartésienne
:
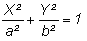
Nous pouvons aussi définir l'ellipse à partir de ses
foyers A et B.
M étant un point de l'ellipse, la longueur de la corde ABMA
est constante.
Nous retrouvons ci-dessous, la méthode des jardiniers pour
tracer cette courbe.

Avec
une corde de longueur constante
On déplace le point M en tirant sur la corde dont la longueur
reste constante.
Cette corde est fixée sur les deux points fixes A et B qui
sont appellés les foyers de l'ellipse.
Dans la première animation, le point M se déplace
en laissant sa trace qui dessine une ellipse de foyers A et B.
Dans la deuxième animation, le point se déplace sur
l'ellise tracée préalablement.
Dans chacun des deux cas, on peut déplacer les points A et
B, de même que le sommet S.
Si les animations suivantes ne tournent pas, mettez à jour
la machine virtuelle Java ici :
http://www.java.com/fr/download/manual.jsp
Si l'animation
s'arrête, replacer la souris dans le cadre.
Pour déplacer soi-même le point M,
cliquer d'abord à l'intérieur du cadre pour le stopper,
le déplacer ensuite,
il redémarrera seul, avec un nouveau clic intérieur
au cadre.
