Etoile d'or et rectangle d'or à partir d'un arc en tiers point

Le merveilleux arc brisé en tiers-point,
hexagone régulier, étoile d'or et rectangle d'or

La construction

Cette construction m'a été proposée par Patrick Garnier avec une question :
Cette construction est-elle,
- parfaitement rigoureuse ou bien
- juste une trè bonne approximation ?

Patrick Garnier (Provence-Alpes-Côte d'Azur, qui étudie les tracés régulateurs au Moyen-Âge et notamment les plate-tombes médiévales), l'a mise en évidence suite à son étude sur la plate-tombe (*) de Hugues Libergier (cathédrale de Reims XIIIème siècle) et notamment du compas de ce célèbre maître d'œuvre de l'ancienne église Saint-Nicaise à Reims.

Le départ de la recherche de Patrick Garnier fut tout d’abord un petit dessin du carnet de croquis de Villard de Honnecourt qui comportait cette légende écrite en vieux français Picard: "voici comment l’on fait trois manières d’arcs avec la même ouverture de compas".

Ici, il s’agit d’un plein cintre , d’un arc brisé en tiers-point et d’un arc ogival.
Patrick s'interroge :
"On sait que Villard de Honnecourt est passé à Reims ; a-t-il rencontré un Maître ?
Libergier peut-être ? connaissait-il ce compas ?
Il semble par ce dessin qu’il en suggère sa connaissance et son implication géométrique …"

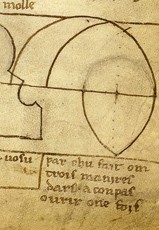Croquis de Villard de Honnecourt

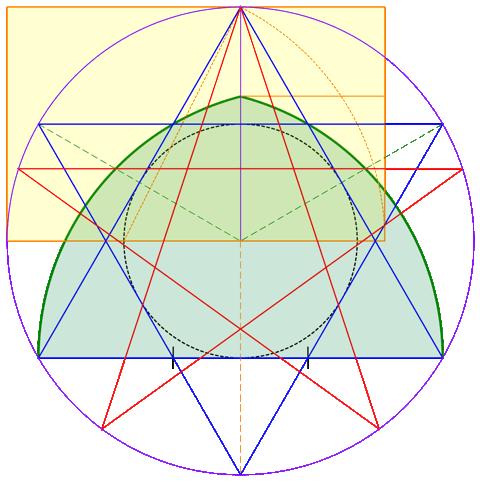
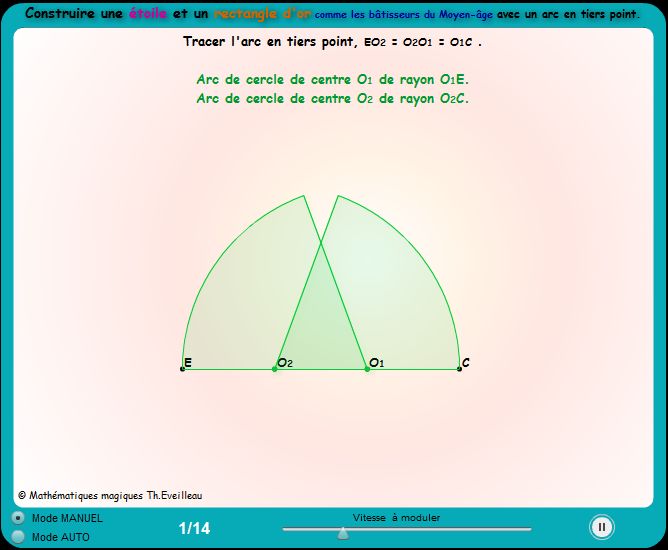
Animation pas à pas ou automatique de la construction avec un arc brisé en tiers-point

Cette animation traduit avec des moyens modernes une construction utilisée par les bâtisseurs du Moyen-Âge.
Source: Hugues Libergier, architecte rémois (1229 - 1263), bâtisseur de cathédrales.

J 'ai utilisé des arcs de cercle pour repérer les points utiles (donc seulement le compas et la règle).
Les propriétés mathématiques de la construction sont inchangées.

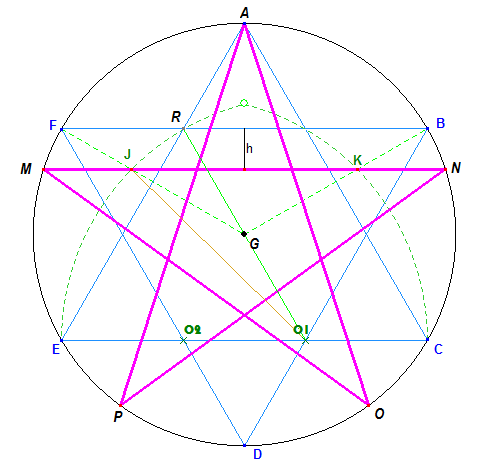
Cette construction permet de tracer un pentagone régulier en passant entre autres par un hexagone régulier, ce n'est pas courant.

CLIQUER

Question

Pouvez-vous répondre à l'interrogation de Patrick Garnier :
cette construction est-elle parfaite ou bien est-ce une très bonne approximation ?
Obtient -on un pentagone régulier parfait à partir de l'arc en tiers-point puis de l'hexagone régulier ?
Justifier la réponse.

Réponse et démonstration
Retrouvez ce problème avec Diophante sous le n° D1810.

La construction est parfaitement rigoureuse.
Soit r le rayon du grand cercle, prenons-le comme unité de longueur.

Ainsi r = 1.

Φ est le nombre d'or : .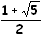
Nous allons démontrer que le rapport de la diagonale du polygone (AMPON) sur le rayon du cercle circonscrit est .
Cette propriété prouve que le polygone est un pentagone régulier avec la realtion :
MN / AM = Φ .

Ceci démontrera que le polygone (AMPON) est un pentagone régulier parfaitement construit.

La démonstration est un peu technique et calculatoire...

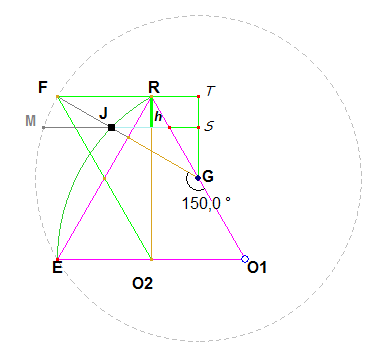
Nous avons O1R = O1E = 2 O1O2.
GE = GF = r = 1.
Notons que GF est bissectrice de l'angle BFD = 60° et il s'ensuit (avec le triangle isocèle FRG) que l'angle FGO1 mesure 150°.

Calculons JF
Comme O1R est le côté d'un triangle équilatéral de hauteur GE = 1, nous déduisons que :
O1R = O1E = O1J = 2/ 3 et comme O1G = O1R / 2 nous obtenons
O1G = / 3.

Avec la formule d'Al-Kashi (théorème généralisé de Pythagore) dans le triangle FGO1, nous écrivons :
O1F² = GF² + O1G² - 2 * GF*O1G*cos(150°)
c'est à dire :
O1F² = 1² + O1G² - 2 * O1G * cos(150°)

De même dans le triangle dans le triangle JGO1,
nous écrivons :
O1J² = O1G² + GJ² - 2 * O1G * GJ * cos(150°)
c'est à dire :
GJ² = O1J² - O1G² + 2 * O1G * GJ * cos(150°)
GJ² = O1E² - O1G² + 2 * O1G * GJ * cos(150°) soit
GJ² = O1E² - O1G² + 2 * O1G * GJ * cos(150°)
Posons x = GJ avec x>0, Il vient
x² = 2(/ 3) ² - (/ 3) ² + 2 (/ 3) * x * cos(150°)
soit
x² = 4 / 3 - 1 / 3 + 2 (/ 3) * x * cos(150°)
soit
3x² - 2x * cos(5 π/6) - 3 = 0 qui devient
3x² + 2x * cos(π/6) - 3 = 0 OU encore
3x² + 2x /2 - 3 = 0 et donc

x² + x - 1 = 0
dont la racine positive est x = ( - 1 + ) / 2
Finalement
GJ = ( - 1 + ) / 2

Maintenant JF = GF - GJ = 1 - x = 1 - ( - 1 + ) / 2
d'où
JF = ( 3 - ) / 2 .
Par ailleurs,
h = FJ * sin (30°) donc h = 0.5 * ( 3 -) / 2
soit
h = ( 3 -) / 4 .

Nous allons maintenant déduire MN à partir de FB par proportionnalité avec le théorème de Thalès.
Nous avons FB = r
(cela vient du triangle équilatéral FBD dont la hauteur est 1.5 r ).

Et comme nous avons posé r = 1,
FB = .

Avec le théorème de Pythagore dans le triangle rectangle GSM :
GM² = GS² + MS² (relation *)

Par ailleurs, avec GT = r / 2 = 1 / 2 (car G est centre de gravité du triangle équilatéral FBD) :
GS = GT - h = 1/2 - (3 - ) / 4= 1/2 - 3/4 + / 4 = ( -1 + ) / 4
GS = ( - 1 ) / 4

et GM = r = 1

Avec la relation * nous obtenons
MS² = GM² - GS² = 1 - ( ( - 1 ) / 4) ) ² = 1 - (5 +1 - 2) / 16 = 1 - (6 - 2) / 16 = (5 + ) / 8
MS² = (5 + ) / 8 et cela implique
MS = () / 2 et finalement

MN = ()

C'est ce que nous voulions démontrer, CQFD.

Nous avons un pentagone d'or parfait et la construction est rigoureuse.
La construction du rectangle qui suit respecte les rapports du rectangle d'or. Elle est également rigoureuse et parfaite.

BRAVO aux bâtisseurs du Moyen-Âge.