Un
billard triangulaire équilatéral
Le
problème Sur
l'idée du n°I165
de Diophante.fr
| Une
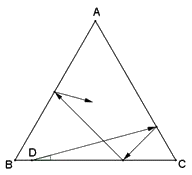
table de billard a la forme d'un triangle équilatéral
ABC d'un mètre de côté.
On place une boule (assimilée à un point) en un
point D du côté BC à 10 cm de B.
La frappe de la boule se fait selon un angle inférieur
à 90° mesuré dans le
sens anti horaire par rapport à la droite BC.
On s'intéresse aux seules trajectoires de la boule qui
rebondit sur les côtés du triangle
selon la loi classique de la réflexion avant de revenir
pour la première fois à son point
de départ D.
Q1 Déterminer
les trajectoires distinctes qui ont exactement 21 mètres
de longueur.
Pour chacune d'elles, donner l'angle de frappe et le nombre de
rebonds* de la boule.
Q2 Une nouvelle frappe de la boule donne
90 rebonds* avec une longueur de la trajectoire qui s'exprime
encore en un nombre entier de mètres.
Déterminer la ou les trajectoires correspondantes (longueur,
angle de frappe).
|
|
*Nota: tout rebond
correspond au changement de direction de la boule en un point intermédiaire
de sa trajectoire
L'arrivée en D compte pour un rebond mais pas le départ
de D. 
ANIMATION
Pour
une bonne compréhension de la trajectoire de la boule, voici
une modélisation que chacun pourra paramétrer à
sa guise.
Nous allons de plus ici, essayer de repérer les trajectoires
périodiques.
Dans cette animation
il faut donner,
-
l'angle de frappe au départ:
: frapper ce nombre au CLAVIER en utilisant
un point pour la virgule.
On peut entrer jusqu'à 7 décimales.
C'est important dans le cas des questions Q1 et
Q2 du problème ci-dessus.
il est souhaitable d'entrer au moins 5
décimales pour obtenir le bon test d'arrêt
pour un nouveau cycle périodique (angle et position).
Dans certains cas 4 décimales sont suffisantes
mais pour 90 rebonds, 7 sont nécessaires
quand d=0.5..
Plus
le nombre de rebonds est important pour revenir à la case de
départ, meilleure doit être la précision de l’angle
d’attaque.
- la position de la boule au départ
sur la base horizontale du triangle.
- Le bouton RAZ permet de tout réinitialiser
; on peut alors modifier la position et l'angle de frappe de la boule.
- le bouton GO fixe les paramètres et en appuyant
sur la flèche on lance l'animation.
On peut avancer pas à pas avec le mode MANUEL, ou laisser le
mode AUTOmatique agir.
Dans ce dernier cas, lorsque la boule revient au point de départ
et reprend la direction initiale, on peut poursuivre en appuyant sur
la flèche et vérifier ainsi que la trajectoire se superpose
à celle déjà parcourue.
- le bouton COULEURS permet de colorier aléatoirement
les segments de la trajectoire de la boule.
Dans
la réalité, le seul moyen parfait de réalisation
serait d'envoyer un rayon lumineux sur un billard équilatéral
composé de miroirs.
Choix effectués
Une assez grande précision, pour éviter d'indiquer
une orbite faussement périodique :
--> les tests sont faits à 0.5 pixel près
pour la position de la boule par rapport au départ ;
le côté mesurant 440 pixels, la précision est de
1/880ème.
--> le test se fait également sur l'angle
en ce même point : la boule doit repartir dans la même direction.
Si
la trajectoire repasse par le même point avec une direction différente
de la direction de départ, on
ne sait pas vraiment ce qu’elle va faire dans le futur.
L'angle de frappe doit donc être très précis.
On sait que :
pour
des valeurs quelconques de l'angle d'attaque de la
boule, et de l'abscisse du point de départ D, la boule ne revient
jamais à son point de départ : il n'y a pas de
trajectoire périodique.
Tester par exemple :
- les valeurs obtenues dans la résolution qui
suit ce paragraphe ;
- un angle de frappe de 60° avec une distance de 0.1 puis de 0.5
;
- un angle de 20° avec une distance de 0.1 donnant un mouvement
perpétuel.
Bientôt
des billards pour mathématiciens : polygones réguliers
et elliptiques.

REMARQUES
On dit qu’une trajectoire du
billard est périodique si au bout d’un certain temps la
boule repasse
par le même
point avec
la même direction
(on dit aussi : orbite périodique).
ATTENTION, la direction doit être la même pour qu’ensuite
la trajectoire se répète indéfiniment.
La longueur d’une trajectoire périodique est la distance
effectuée par la boule pour revenir à sa position initiale
avec sa direction de départ.
Katok (professeur à l’université Penn state aux
Etats Unis et spécialiste de systèmes dynamiques) a posé
la question suivante :
"Est ce que, dans TOUT triangle, il y a (au moins) une trajectoire
de billard périodique ? ".
C'est un problème ouvert qui
n'a aujourd'hui pas de réponse.
Dans un triangle quelconque, on sait qu'il existe une trajectoire périodique
: le triangle orthique,
joignant les pieds des hauteurs du triangle.
Voir ICI.
Dans TOUT triangle, dont le plus
grand angle est inférieur à 100 degrés, Schwartz
montre qu'il y a une trajectoire de billard périodique.
Intéressons-nous
au triangle équilatéral
Pour des valeurs quelconques de l’abscisse de D et de l’angle
d’attaque, le rayon ne revient jamais à son point de départ.
La trajectoire est
périodique avec un angle α de frappe, si et seulement on
a l’équation tan( α ) = r / racine(3) avec
r nombre rationnel positif qui s’exprime en fonction
de Px
et de Py selon les notations qui suivent dans l'analyse ci-dessous.
Exemple de mouvement perpétuel rappelant certaines fractales
:


ANALYSE et résultats
| Q1
Nous allons travailler sur un treillis composé de triangles
équilatéraux de côté l'unité.
On reporte un certain nombre de fois le triangle ABC en utilisant
des symétries par rapport à chacun de ses côtés.
On reporte aussi le nom des sommets : le symétrique de
A étant noté aussi A.
De même pour B et C.
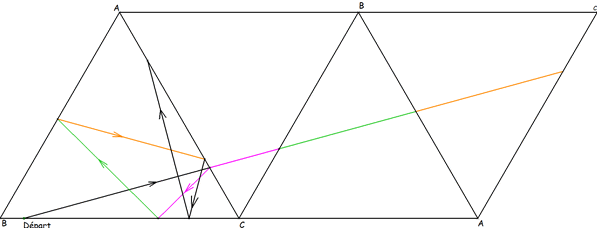
En reportant symétriquement par rapport au côté
du triangle équilatéral le
segment figurant le trajet de la boule au rebond suivant
on obtient une ligne droite sur laquelle nous allons travailler.
Sur la figure ci-dessous les segments de même couleur sont
de même longueur.
Ils correspondent chacun à un rebond d'un côté
sur le suivant.
On peut poursuivre ainsi pour figurer le trajet complet de la
boule sur le billard.
Le trajet complet de la boule est représenté par
une ligne droite sur le treillis.
|

|
|
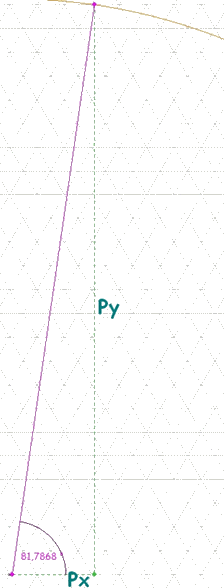
Le problème ICI
: la boule doit revenir au point de départ.
Donc la ligne droite se terminera en un point F sur le côté
BC d’un des triangles.
F correspond au point de départ D = Départ
et sera tel que FB = DB et FC = DC.
| 
|
Soit
Px
la longueur du côté horizontal du triangle
rectangle d’hypoténuse la longueur 21 parcourue.
Soit n le nombre de bases entières de cette projection Px
horizontale. Soit
Py la
longueur du côté vertical du triangle rectangle d’hypoténuse
la longueur 21 parcourue.
Soit k le nombre de lignes horizontales traversées par
la ligne droite de parcours (c’est le nombre de triangles
équilatéraux entiers contenus dans Py.
L’angle sera l’arc dont la tangente est : (Py/Px).
Soit d la distance du point de départ
au bord gauche B.
Dans notre cas d=0.1.
La boule doit finir son parcours en F qui se trouve sur un côté
BC horizontal,
Si n est un nombre
entier de côtés
------------------------------------------------------
Nous obtenons la projection horizontale :
Px =
n + (1 - d ) + d = n + 1
Et la projection verticale :
Py =
k 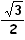
Nous obtenons : Px²
+ Py² = n
² + 1 + 2n + 3k² /4 = 21²
SOIT 4n²
+ 3k² + 8n = 1760
Les seuls couples (n,k) entiers tels que Px²
+ Py² =
21² sont
k = 24 et n = 2 donnant Px
= 3 ET Py=
24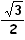
L’angle est environ
81.786°
Le nombre de rebonds est
48.
|
Si
nous avons n entier côtés de base plus un demi-côté
----------------------------------------------------------------------------------
Nous obtenons la projection horizontale :
Px = n
+ 0.5+ (1 - d ) + d = n + 1.5
Et la projection verticale :
Py = k
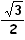
Il
s'ensuit :
Px² + Py²
= n ² + 1.5² + 3n + 3k² /4 = 1760
SOIT 4n²
+ 3k² + 12n = 1755
Donc
deux autres solutions :
k=15 ; n=15 -->
Px
= 16.5 ET
Py=
15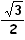
L’angle est environ 38.21321°
Le nombre de rebonds est 48.
PUIS
k=9 ; n=18 -->
Px
= 19.5 ET
Py=
9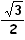
L’angle est environ 21.7867°
Le nombre de rebonds est 48.
|
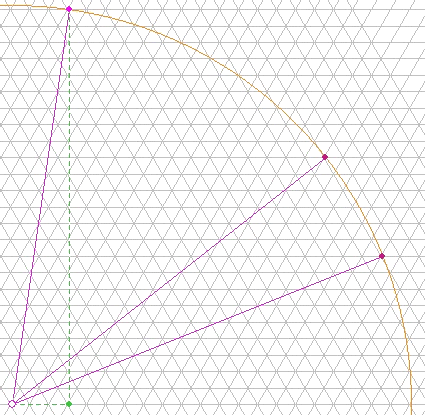
FINALEMENT nous avons trois solutions représentées
ci-dessus. |
Les rebonds sont décomptés en dénombrant les intersections
de la trajectoire droite de la boule avec les droites du réseau
triangulaire.
Q2
Nous
raisonnons de la même façon pour obtenir trois solutions
avec 90 rebonds.
Tester
ces résultats avec l'animation ci-dessus.
ATTENTION
il est préférable de donner au moins 5 décimales
pour l'angle de frappe.
(*) Pour
une explication complète
des calculs aller sur Diophante.fr
ICI.
Et plus sur le billard équilatéral
ICI :
http://www.diophante.fr/images/stories/diophante/decembre_2018_2/I165AB.pdf
|

 PLEIN
ECRAN
PLEIN
ECRAN