Un vrai voyage de découvertes ne consiste pas à rechercher
de nouveaux horizons mais à avoir un nouveau regard.
Marcel Proust
![]() La
SIMULATION
La
SIMULATION
On fait partir une boule rouge d'un coin du billard pour atteindre une
cible verte.
La boule doit rebondir un nombre de fois fixé à l'avance
sur les côtés du billard.
Quelle direction donner à la boule ?
Ci-dessous positionner avec la souris la cible verte à l'intérieur
du billard, puis fixer le nombre de rebonds.
Observer la direction initiale de la balle et essayer de conjecturer.
CLIQUER
![]() COMPRENDRE
COMPRENDRE
Le plus court
chemin, c'est la ligne droite ! Nous en avons déjà parlé
dans la page des pompiers.
Une boule de billard, lancée d'un point donné rebondit (comme
un rayon lumineux) en faisant un angle symétrique à celui
par lequel elle est arrivée.
Elle suivra le chemin le plus court vers le point désiré.
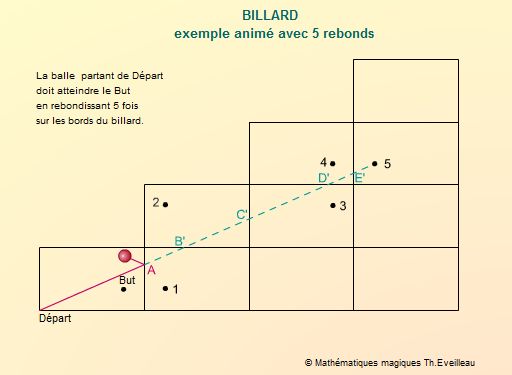
Dans la première animation ci-dessous, nous cherchons à
viser le but après 5 rebonds sur les côtés.
Construisons des rectangles identiques autour du billard puis les symétriques
des points visés en partant du But donc de la fin du parcours
désiré.
Nous obtenons sur les rectangles annexes, la ligne droite AB'C'D'E',
distance la plus courte de Départ vers But.
Des segments symétriques ayant la même longueur, on obtient
le véritable chemin ABCDE suivi par la boule sur billard.
Dans l'animation ci-dessous, on peut modifier au départ la position
de la balle et choisir le nombre de rebonds.
Pour des raisons pratiques, les symétriques sont construits successivement
autour de chacun des côtés du billard.
Toutefois l'analyse reste la même.
Si la balle frappe un coin... elle sort !
CLIQUER
![]() BILLARD
TRIANGULAIRE
BILLARD
TRIANGULAIRE
Peut-on trouver
une trajectoire pour une boule de billard ou un rayon de lumière
qui boucle en une seule fois ?
La réponse est affirmative dans le cas où l'orthocentre
est intérieur au triangle (les trois angles sont aigus).
La trajectoire passe par les pieds des hauteurs du triangle.
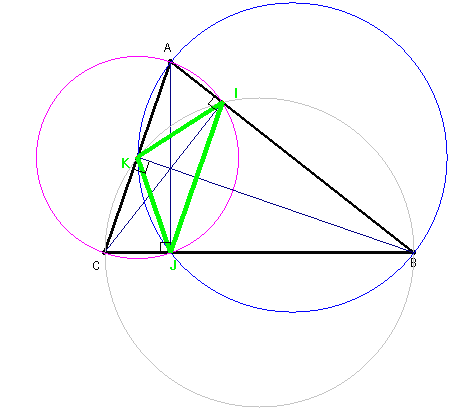
Sur la figure ci-dessus, le trajet de la lumière est dessiné
en vert. C'est le triangle orthique
de ABC.
Pour le démontrer on peut observer que les points A, I J et C sont
sur le cercle de diamètre [AC]
(propriété du triangle rectangle inscrit
dans un demi-cercle de diamètre l'hypoténuse de ce triangle).
Alors les angles inscrits AIJ et ACJ sont supplémentaires.
De la même façon, les points K, I, B et C sont cocycliques
(cercle de diamètre [BC] ),
donc les angles inscrits KIB et KCB (=ACJ) sont supplémentaires.
On en déduit l'égalité des mesures des angles AIJ=AIK+KIJ
et KIB=BIJ+KIJ.
Finalement on a l'égalité AIK=JIB. Il en est de même
pour les angles sur les autres côtés.
CQFD.
Pour aller beaucoup plus loin, voir
le théorème de la baguette magique de A. Eskin et M. Mirzakhani
qui a valu la médaille Fields à Maryam Mirzakhani :
https://docplayer.fr/88462078-Le-theoreme-de-la-baguette-magique-de-a-eskin-et-m-mirzakhani.html