Le problème

Supposons que dans une chambre, dont le parquet est simplement divisé par des joints parallèles, on jette en l'air une aiguille, et que l'un de deux joueurs parie que l'aiguille ne croisera aucune des parallèles du parquet, que l'autre au contraire parie que l'aiguille croisera quelques unes de ces parallèles ; quel est le sort des deux joueurs ?
On peut jouer ce jeu sur un damier avec une aiguille à coudre ou bien une épingle sans tête.

Georges Louis Leclerc de Buffon (1707-1788) est connu essentiellement pour son œuvre de naturaliste. Cet administrateur qui agrandira et enrichira le jardin du Roi, membre de l'Académie Française et de toutes les grandes académies européennes, fut aussi philosophe et mathématicien.
C'est dans son Essai d'arithmétique morale publié en 1733 que l'on peut trouver le "mémoire sur le jeu du franc carreau" qui contient le fameux problème de l'aiguille.
Il a montré que la probabilité qu'une aiguille de longueur L, lancée sur un parquet dont les lattes ont une largeur L, coupe le bord d'une latte est . Dans le cas général, pour une aiguille de longueur a et des lattes de largeur b, la probabilité est .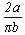
C'est la première fois que la géométrie apparaît en termes en probabilités.
Et curieusement ce problème lié au nombre π, rapproche des domaines mathématiques apparemment éloignés.


Si vous avez des trésors de patience, lancez un très grand nombre de fois une aiguille sur le parquet et notez la fréquence relative d'intersections (nombre d'intersections divisé par le nombre de lancers), vous obtiendrez une évaluation de .
La Loi des grands nombres assure que cette fréquence relative tend vers la probabilité lorsque le nombre d'aiguilles tend vers l'infini...
Il ne faut pas se faire d'illusions... pour obtenir une bonne valeur de π avec cette technique, disons avec la précision au millième, donc 3,142 avec une probabilité de 95%, on doit lancer environ… 900 000 aiguilles !
La méthode ne converge pas vite...
Aussi, je vous propose de faire cette expérience de manière moins fastidieuse avec une simulation.

Dans l'animation suivante,

on peut interrompre momentanément le tirage aléatoire pour noter la valeur approchée de π obtenue, puis poursuivre le tirage ou bien recommencer une nouvelle expérimentation.

CLIQUER

 

 

Dans l'animation suivante, on entre le nombre de lattes simplement.

On ne voit plus ni les lattes ni les aiguilles, mais la valeur de π est constamment mise à jour avec le nombre d'aiguilles jetées.
On recommence l'expérience quand on veut.

CLIQUER puis OUVRIR puis DOUBLE CLIQUER le fichier

Cette fois, on entre le nombre de lattes et le nombre d'aiguilles.

On ne voit plus ni les lattes ni les aiguilles, mais la valeur de π est beaucoup plus rapidement calculée.
Il faut attendre un tout petit peu si le nombre est très grand.
On peut recommencer ensuite.

CLIQUER

 

 

Démonstrations

.Celle d'Emile Borel assez simple
Le nombre d'aiguilles qui tombent en coupant une ligne est proportionnel à la longueur des aiguilles, notée a, et inversement proportionnel à la distance b entre les lattes (entre les lignes du réseau). Cela peut s'écrire sous la forme suivante : , où k est une constante à déterminer.
Pour déterminer la constante k, imaginons une aiguille en forme d'anneau, de diamètre b. Sa longueur, qui est en fait sa circonférence, est π b.
Peu importe où elle tombe, puisque son diamètre est égal à l'écart existant entre deux lignes parallèles, elle coupe toujours deux fois les lignes.
On en déduit donc que = 2, puis que = 2 (vu que, a = πb), ce qui nous donne finalement : k = .
La probabilité cherchée est donc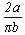

.Démonstration classique
Désignons par y (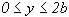) la distance du milieu I de l'aiguille et par θ () l'angle de l'aiguille avec la direction des lattes.

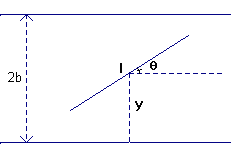
Il y aura intersection 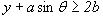si ou si .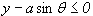
Le point P(θ,y) doit donc appartenir à la zone colorée en jaune dans le graphique ci-dessous.

Or la distribution de q sur [0, π/2] et de y sur [0, 2b] est uniforme.
Il s'ensuit que la probabilité cherchée est le rapport de l'aire de la surface colorée en jaune à l'aire du rectangle [0, θ/2] x [0, 2b] (qui représente tous les cas possibles).
L'aire du rectangle est
2 b x π /2 = π b.

Les deux parties hachurées sont symétriques et ont même aire.
L'aire hachurée est donc :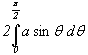


Finalement la probabilité est :

Voir aussi :
Archimède π Eureka
Pour en savoir plus voir JEAN-PAUL DELAHAYE Le fascinant nombre π Bibliothèque Pour la Science, Belin.