| Les
clés de détection d'erreur
 Numéro
INSEE Numéro
INSEE
Quels
sont les numéros corrects dans la liste suivante ?
 |
2
55 08 14 168 025 12
1 77 09 76
451 032 10
2 82 12 75 114 123 14 |
Le
numéro de sécurité sociale de chacun est composé
de quinze chiffres. Les deux derniers forment une clé de deux
chiffres.
Le premier donne le sexe (1 pour masculin, 2 pour féminin), les
deux suivants l'année de naissance (2 derniers chiffres du millésime),
puis le mois (sur 2 chiffres : février donne 02), le numéro
du département (99 pour l'étranger, 2A et 2B pour la Corse
: des règles spécifiques sont utilisées pour calculer
la clé en Corse), celui de la commune (3 chiffres) enfin le numéro
d'ordre d'inscription sur le registre d'état civil (3 chiffres).
Les deux derniers constituent la clé de vérification.
Celle-ci est calculée à partir du nombre formé
par les treize premiers chiffres. Si celui-ci a pour reste n dans la
division par 97 alors la clé sera 97 - n.
Pour la Corse,
-on remplace le caractère A ou B par un zéro.
-si la lettre est A, on soustrait au nombre de 13 chiffres la valeur
1 000 000 et si la lettre est B on soustrait 2 000 000.
- ensuite on effectue le calcul indiqué proposé ci-dessus.
Sur le plan pratique il suffit d'ajouter le nombre formé des
treize premiers chiffres et celui formé des deux derniers chiffres
pour vérifier une clé. Ce nombre devra être un multiple
de 97.
Exemple
2 55 08 14 168 025 38 est un numéro correct :
sexe féminin, née en 1955 au mois d'août
dans le Calvados à Colombières la 25ème.
59 étant le reste de 2550814168025 dans la division par 97.
La
clé est 38 = 97 - 59.
On vérifie que 2550814168025 + 38 = 2550814168063 est un multiple
de 97.
Afin
d'éviter de longs calculs, entrez dans le premier cadre le début
à 13 chiffres du numéro d'INSEE pour obtenir le reste
dans la division par 97 ou bien le numéro à 15 chiffres
pour vérifier la clé.
Ensuite modifiez un chiffre ou échangez deux chiffres et observez
l'influence sur la détection d'erreur.
CLIQUER

CLIQUER

La
clé permet de détecter les erreurs d'écriture les
plus fréquentes.
Ce nombre 97 offre de nombreuses clés différentes possibles
(de 1à 97).
Par ailleurs ce nombre étant premier permet de détecter
certaines erreurs provenant du remplacement d'un chiffre par un autre
ou de permutations.
 Numéro
ISBN Numéro
ISBN
Quels
sont parmi les numéros suivants ceux qui sont des numéros
ISBN ?
 |
2
8769 4033 7
0 486 20498 7
0 8228 8315 8 |
L'ISBN
(International Standard Book Number) est un numéro
international normalisé qui permet d'identifier le titre d'un
livre.
Ce numéro de 10 chiffres est composé de 4 parties.
La première correspond à la zone linguistique : 2 pour
le français ; la deuxième indique l'éditeur; la
troisième correspond au numéro d'ordre dans la production
de l'éditeur et enfin la dernière partie (chiffre ou lettre)
correspond à la clé de contrôle.
On donne un ISBN pour une série complète et un ISBN distinct
pour chaque exemplaire composant la série.
Cette clé est notée
· au verso de la page de titre, au bas de la dernière
page de couverture et au bas de la dernière page de la jaquette
des livres
· sur l'étiquette des documents électroniques et
logiciels (cassettes, disquettes...) ainsi que sur la dernière
page de couverture du manuel de l'utilisateur et de l'emballage
.sur la dernière page de couverture des boîtes et boîtiers
des cassettes non musicales et des vidéocassettes.
Exemple
2-212-09265-2
pays francophone,
éditions Eyrolles, numéro d'ordre 09265, clé
: 2.
La
clé est le reste dans la division par 11, (voir aussi la preuve
par 11) d'un nombre intermédiaire N calculé
à partir des neuf premiers chiffres de l'ISBN. Si ce reste est
10 la clé sera notée X.
N est obtenu en multipliant par 1 le premier chiffre de gauche, puis
on lui ajoute le second multiplié par 2, puis le troisième
multiplié par 3 et ainsi de suite ... jusqu'à ajouter
le neuvième que l'on a multiplié par 9.
Sur l'exemple 2-212-09265-2
le calcul intermédiaire donne N = (1x 2) +(2 x 2)
+(3 x 1) + (4 x 2) + (5 x 0) + ( 6 x 9)
+ (7 x 2) + (8 x 6) + (9 x 5) = 178
et 178 a pour reste 2 dans la division par 11, la clé est donc
2.
CLIQUER
CLIQUER

 Les
codes barres Les
codes barres
Utilisé
pour la gestion et la vente de produits. Nécessite un lecteur
de codes barres.
Le premier code barres a été breveté le 7 octobre
1952 par les Américains Norman Woodland et Bernard Silver.
Au lieu des barres verticales actuelles, ils avaient imaginé
des cercles concentriques (première apparition à Ohio
en 1974)
 . .
Aujourd'hui, nous avons une série de barres noires codées
en système binaire avec des 0 (absence de barre) et des 1 (présence
de barre).
Il existe de nombreuses normes de codes barres (code 128, code 39,
Codabar...).
Nous analyserons ici le code EAN-13. Il s'agit du sigle correspondant
à European Article Number
créé en 1976.
30
barres représentent 13 chiffres organisés en
trois parties (on peut utiliser jusqu'à 15 ou 18 chiffres).

-la
première partie comporte 2 chiffres donnant les deux premiers
chiffres du code pays : bonne astuce pour consommer local,
(50 --> Grande-Bretagne ; 84 --> Espagne, 35 --> France).
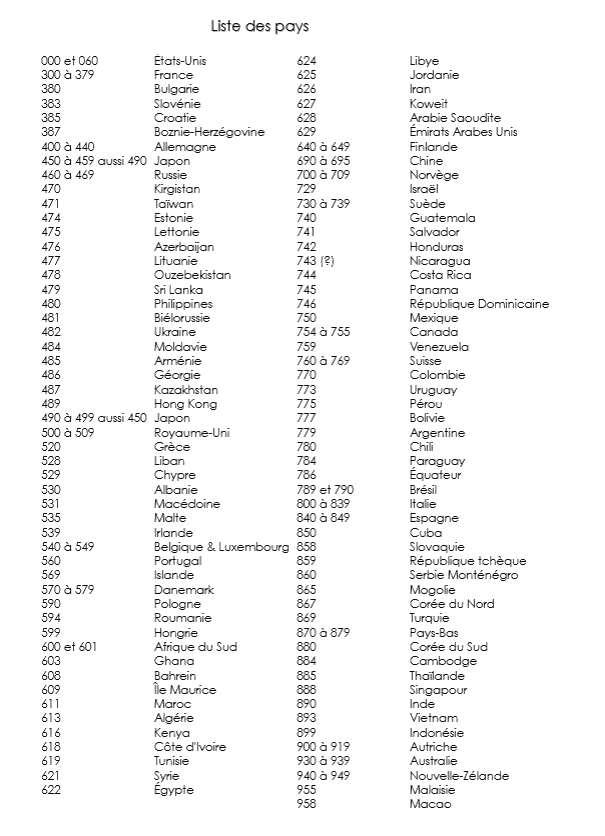
-la deuxième partie comporte 5 chiffres identifiant
le code de l'entreprise productrice : ici 10356
-la troisième partie comporte 5 chiffres identifiant
le code du produit défini par l'entreprise: ici 82335
-le dernier chiffre est la clé de contrôle,
ici 7.
Pour calculer la clé de contrôle, il faut
. ajouter les chiffres de rang impair en partant de la gauche et ne
pas compter le dernier chiffre de contrôle ;
. Ajouter à ce résultat trois fois la somme des chiffres
de rang pair toujours en partant de la gauche.
On obtient R.
la clé de contrôle est le chiffre (entre 0 et 9) qui
ajouté à R va donner un multiple de 10.
Exemple avec le code :
5 0 1 0 3 5 6 8 2 3 3 5 7
( 5 + 1 + 3 + 6 + 2 + 3) + 3 (0 + 0 + 5 + 8 +3 + 5) = 20 +( 3 x 21
)
On obtient 83 et nous devons ajouter 7 pour
obtenir 90 qui est le premier multiple de 10 après 83.
Le code précédent est bien correct.
Une autre façon de procéder est de vérifier que
le code est correct en utilisant tous les caractères.
:Il faut obtenir un multiple de 10 :
( 5 + 1 + 3 + 6 + 2 + 3 + 7) + 3 (0 + 0
+ 5 + 8 +3 + 5) = 90.
90 est bien un multiple de 10, le code est correct.
CLIQUER
Les codes QR
Ce
code est un pictogramme de type matriciel comportant un nombre variable
de petits carrés blancs et noirs constituant eux-mêmes
un carré plus grand.
Les carrés représentent des valeurs binaires : 0 ou
1.
Le fonctionnement est donc similaire aux codes barres, il propose
cependant un stockage beaucoup plus grand.
Il permet entre autres
. un lien rapide vers un contenu en ligne ;
. des échanges de coordonnées ;
. le paiement ;
. suivi de lots ou de pièces etc.
Pour le saisir il faut des capteurs spéciaux ou un smartphone
avec l'application Flashcode.
Si elle n'est pas déjà installée sur votre smartphone,
vous pouvez télécharger cette application gratuitement.:
Vous
pouvez essayer de flasher le code suivant.


  Numéro
de compte bancaire
puis numéro de carte bancaire Numéro
de compte bancaire
puis numéro de carte bancaire
Un compte en banque est identifié par 23 caractères qui
sont pour la plupart des chiffres. On les trouve sur le relevé
d'identité bancaire (le rib) . Le nombre
formé par les deux derniers chiffres de droite constitue
la clé permettant de vérifier la cohérence du numéro.Les
21 premiers caractères sont formés par :
-le
code de banque (5 chiffres)
-le code du guichet ou de l'agence (5 chiffres)
-le numéro de compte proprement dit.
Si l'un des caractères est une lettre, il faut le coder à
l'aide de la correspondance donnée dans le tableau suivant.
| A |
B |
C |
D |
E |
F |
G |
H |
I |
| J |
K |
L |
M |
N |
O |
P |
Q |
R |
| |
S |
T |
U |
V |
W |
X |
Y |
Z |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Si on désigne
par N le nombre de 21 chiffres construit comme indiqué ci-dessus,
la clé de contrôle C est calculée par la formule
C = 97 - reste de la division de 100*N par 97.
Ce nombre C doit être
écrit avec deux chiffres.
S'il est plus petit que 10, il faut écrire un zéro à
sa gauche.
Exemple : 4 devient 04.
En écrivant la clé de contrôle C, avec deux chiffres,
juste à droite du nombre N initial, on doit donc obtenir un multiple
de 97 (la division par 97 tombe juste).
Exemple
| Banque |
Guichet |
Compte |
Clé |
| 18208 |
00003 |
01170928519 |
13 |
Ci-dessous, vous
pouvez entrer et vérifier vos ribs. Il est possible d'entrer
un numéro de compte avec des lettres.
CLIQUER

CLIQUER


 Numéro
de carte bancaire Numéro
de carte bancaire
Le numéro d'une carte bancaire est composé de 16 chiffres,
clé comprise.
Dans ce numéro, interviennent
-le type de carte,
-le numéro de la banque.
Un algorithme particulier permet aux banques de composer le numéro
de la carte bancaire. Ce numéro varie selon l'organisme bancaire.
Le seizième chiffre correspond à la clé qui permet
de valider la carte.
C'est l'algorithme de Luhn qui permet de déterminer
cette clé. Il permet de vérifier un numéro mais
ne valide pas l'existence de la carte.
Voici
comment trouver la clé à partir du nombre constitué
des quinze premiers chiffres
En partant de la gauche,
-multiplier par deux chaque chiffre de rang impair ; si le résultat
de cette multiplication par deux est supérieur à 9, lui
soustraire 9 ;
-garder les autres nombres tels qu'ils sont ;
-additionner ensuite tous les chiffres obtenus : ceux qui ont été
multipliés par deux et ceux qui n'ont pas été modifiés
;
-prendre le reste R de cette somme dans la division par
dix.
Si ce reste R est nul, le garder comme clé
sinon prendre son complément à dix, la clé
est donc 10 - R.
Exemple
5426 8567 1234 458
ATTENTION, ce numéro
est inventé et non valide comme numéro de carte bancaire.
Il s'agit juste d'un exemple pour le calcul d'une clé selon l'algorithme
de Luhn.
5 x 2 = 10 --> 1
2 x 2 = 4
8 x 2 = 16 --> 7
6 x 2 = 12 --> 3
1 x 2 = 2
3 x 2 = 6
4 x 2 = 8
8 x 2 =16 --> 7
On
ajoute ensuite :
1 + 4
+ 4 + 6 + 7
+ 5 + 3 + 7
+ 2 + 2 + 6
+ 4 + 8 + 5
+ 7
= 71
71
a pour reste 1 dans la division par 10.
La clé est ici égale à 10 - 1 = 9.
CLIQUER

CLIQUER

 Les
billets en euros ? Les
billets en euros ?
Les
billets en euros sont numérotés de façon astucieuse.
Le numéro se présente pour les anciens billets, sous la
forme d'une lettre suivie de onze chiffres, exemple
: Z73585540773.
Pour les nouveaux billets il y a deux lettres suivies
de dix chiffres, exemple : EA4562608096.
Remplaçons d'abord la lettre par son rang dans l'alphabet comme
indiqué dans le tableau suivant :
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
Nous obtenons
un nombre de douze ou treize chiffres. Alors, le reste de ce nombre
dans la division par 9 doit être 8 pour les anciens billets et
7 pour les nouveaux billets.
Une autre façon de procéder est d'ajouter le nombre de
lettres (1 ou 2) au reste dans la division par 9
du nombre correspondant à la partie numérique du numéro
à laquelle
on a ajouté le code de la ou des lettres.
On doit obtenir un multiple de 9 : il doit donner un reste nul dans
la division par 9.
Ainsi
ancien billet (Z a pour code 26) : Z73585540773
donne 1 + 26 + 73585540773
soit modulo 9 --> 1 + 26 + 54 = 81 dont le reste est nul dans la
division par 9 ;
nouveau billet (E a pour code 5 et A a pour code 1) :
EA4562608096 donne 2 + 5 + 1 + 4562608096
soit modulo 9 --> 2 + 5 + 1 + 46 = 54 dont le reste est nul dans
la division par 9.
Consulter
à ce propos la page de Roberto Rolland :
http://robert.rolland.acrypta.com/telechargements/lycees/euro2014.pdf
Remarque :
-pour qu'un nombre soit divisible par 9, il suffit que la somme de ses
chiffres soit divisible par 9.
En pratique, on fait la somme des chiffres, on obtient un nouveau nombre
sur lequel on recommence le procédé et ainsi de suite.
-pour trouver le reste d'une division par 9, il suffit de remplacer
le nombre à diviser par la somme de ses chiffres et de diviser
cette somme par 9.
Exemple : reste de 785486 par 9 ?
.c'est celui de (7+8+5+4+8+6) par 9, donc de 38 par 9, donc aussi de
(3+8) par 9, donc de 11 par 9, donc de (1+1)=2 par 9, c'est donc 2.
Vérifiez vos calculs du reste dans la division par 9 dans le
cadre ci-dessous en entrant un nombre ayant 30 chiffres au maximum.
CLIQUER
Et
ci-dessous vérifiez le numéro de votre billet ou un numéro
que vous inventerez...
CLIQUER


 Le
numéro d'Avis de Contravention Le
numéro d'Avis de Contravention
Ci-dessous,
si vous en avez malheureusement reçu, vous pouvez vérifier
votre N° d'Avis de Contravention.
La
Clé de la contravention figure à droite du N° d'avis
de contravention.
Elle est calculée à partir du nombre formé
par les quatorze chiffres du N° de l'Avis.
ATTENTION
: si votre numéro n'a que dix chiffres, il faut le compléter
en écrivant 333 au début à
gauche et 1 à droite à la fin
du nombre.
Par
exemple 4878767653 devient
33348787676531
La clé est égale au reste de la division du N° à
14 chiffres de l'Avis par 97.
C'est donc un nombre compris entre 0 et 96.
Si ce nombre est plus petit que 10, on écrit un zéro à
sa gauche pour obtenir un nombre de deux chiffres.
Sur
l'exemple précédent, 33348787676531
nous trouvons 58.
Que ce soit à la main ou avec une calculatrice, effectuer la
division par 97 pour trouver le reste d'un très grand nombre
n'est pas très compliqué mais... un peu long et il
y a des risques d'erreurs.
Aussi les animations suivantes vous faciliteront la tâche.
.Dans la première animation, il
suffit d'entrer le numéro de l'Avis d'amende, numéro à
quatorze chiffres, et la clé sera calculée.
.Dans la deuxième animation, entrer
le numéro d'Avis de Contravention avec sa Clé, numéro
à seize chiffres.
Vous vérifierez ainsi si la clé est correcte ou
non.
ATTENTION, la clé a deux chiffres (éventuellement
0 pour le chiffre de gauche).
CLIQUER

CLIQUER

|
 .
. Numéro
de compte bancaire
puis numéro de carte bancaire
Numéro
de compte bancaire
puis numéro de carte bancaire


















